Vecteurs, colinéarité, orthogonalité

Géométrie dans l’espace

Introduction aux vecteurs dans l’espace 🧭

En géométrie dans l’espace, les vecteurs sont des outils fondamentaux qui permettent de représenter des déplacements, des forces, ou toute grandeur ayant à la fois une direction, un sens et une intensité. Contrairement aux vecteurs du plan, les vecteurs de l’espace possèdent trois coordonnées. Un vecteur $\vec{u}$ de l’espace est défini par ses trois coordonnées (x, y, z) dans une base orthonormée $(\vec{i}, \vec{j}, \vec{k})$ .

$\vec{u} = x\vec{i} + y\vec{j} + z\vec{k} = (x, y, z)$

Colinéarité de deux vecteurs 🔄

Deux vecteurs $\vec{u}$ et $\vec{v}$ sont dits colinéaires si l’un est un multiple de l’autre. Mathématiquement, cela signifie qu’il existe un réel k tel que : $\vec{u} = k \times \vec{v}$

En coordonnées, si $\vec{u} = (x₁, y₁, z₁)$ et $\vec{v} = (x₂, y₂, z₂)$ , alors ils sont colinéaires si et seulement si : $\frac{x_1}{x_2} = \frac{y_1}{y_2} = \frac{z_1}{z_2}$

Exemple : Soient $\vec{u} = (2, 4, 6)$ et $\vec{v} = (1, 2, 3)$ . Ces vecteurs sont colinéaires car 2/1 = 4/2 = 6/3 = 2.

Orthogonalité de deux vecteurs 📐

Deux vecteurs $\vec{u}$ et $\vec{v}$ sont orthogonaux si leur produit scalaire est nul : $\vec{u} \cdot \vec{v} = 0$

Si $\vec{u} = (x₁, y₁, z₁)$ et $\vec{v} = (x₂, y₂, z₂)$ , alors : $\vec{u} \cdot \vec{v} = x_1x_2 + y_1y_2 + z_1z_2$

Exemple : Soient $\vec{u} = (1, 2, 3)$ et $\vec{v} = (4, -2, 0)$ . Leur produit scalaire vaut 1×4 + 2×(-2) + 3×0 = 4 – 4 + 0 = 0. Ils sont donc orthogonaux.

Représentation graphique 📊

Voici une représentation de deux vecteurs orthogonaux dans l’espace :

Rendered by QuickLaTeX.com

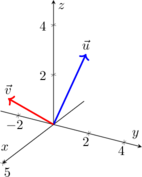
Propriétés importantes 💡

Le vecteur nul 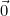$\vec{0}$ est orthogonal à tout vecteur
Deux vecteurs colinéaires ont soit la même direction, soit des directions opposées
La norme d’un vecteur 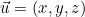$\vec{u} = (x, y, z)$ se calcule par :

$\|\vec{u}\| = \sqrt{x^2 + y^2 + z^2}$

Astuce mnémotechnique 🧠

Pour retenir la condition de colinéarité : « Si les rapports sont égaux, les vecteurs sont parallèles! ». Pour l’orthogonalité : « Produit scalaire nul, angle droit assuré! ».