Transformations géométriques

Accueil » Leçons » Transformations géométriques

Géométrie dans l’espace

Les transformations fondamentales de l’espace 🔄

Les transformations géométriques dans l’espace permettent de déplacer, tourner ou modifier des objets tout en conservant certaines propriétés. Les principales sont les translations, les rotations, les symétries et les homothéties.

Translation 🚀

Une translation de vecteur $\vec{u}$ est la transformation qui à tout point M associe le point M’ tel que :

$\vec{MM'} = \vec{u}$

Si $\vec{u} = (a, b, c)$ , alors les coordonnées se transforment par :

$\begin{cases} x' = x + a \\ y' = y + b \\ z' = z + c \end{cases}$

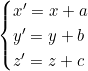
La translation conserve les distances, les angles et les volumes.

Rotation 🔄

Une rotation d’angle θ autour d’un axe Δ est une transformation qui fait tourner les points autour de cet axe.

Pour une rotation autour de l’axe Oz, les formules sont :

$\begin{cases} x' = x\cos\theta - y\sin\theta \\ y' = x\sin\theta + y\cos\theta \\ z' = z \end{cases}$

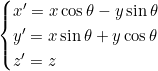
La rotation conserve les distances et les angles.

Symétries 🔁

Il existe plusieurs types de symétries :

Symétrie centrale par rapport à un point O :

$\begin{cases} x' = 2x_O - x \\ y' = 2y_O - y \\ z' = 2z_O - z \end{cases}$

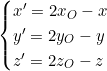
Symétrie orthogonale par rapport à un plan P

Pour un plan d’équation ax + by + cz + d = 0, la symétrie s’exprime par :

$\begin{pmatrix} x' \\ y' \\ z' \end{pmatrix} = \begin{pmatrix} x \\ y \\ z \end{pmatrix} - 2 \frac{ax + by + cz + d}{a^2 + b^2 + c^2} \begin{pmatrix} a \\ b \\ c \end{pmatrix}$

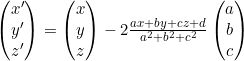
Homothétie 🔍

Une homothétie de centre O et de rapport k (réel non nul) transforme tout point M en M’ tel que :

$\vec{OM'} = k \times \vec{OM}$

En coordonnées, si O(x₀, y₀, z₀) :

$\begin{cases} x' = x_0 + k(x - x_0) \\ y' = y_0 + k(y - y_0) \\ z' = z_0 + k(z - z_0) \end{cases}$

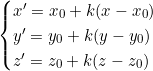
L’homothétie conserve les angles mais multiplie les distances par |k| et les volumes par |k|³.

Représentation d’une rotation 📊

Voici une représentation d’une rotation d’un cube autour de l’axe Oz :

Rendered by QuickLaTeX.com

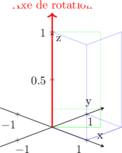
Composition de transformations 🎭

On peut composer plusieurs transformations. Par exemple, une rotation suivie d’une translation. Attention : l’ordre des transformations est important car elles ne commutent pas généralement.

La composition de deux translations est une translation de vecteur somme :

$T_{\vec{u}} \circ T_{\vec{v}} = T_{\vec{u} + \vec{v}}$

La composition de deux homothéties de même centre est une homothétie de rapport produit :

$h_{O,k} \circ h_{O,k'} = h_{O,k \times k'}$

Applications pratiques 🛠️

Les transformations géométriques sont essentielles en :

Infographie 3D : déplacement des objets dans les jeux vidéo
Robotique : calcul des mouvements des bras articulés
Cristallographie : étude des symétries des cristaux
Architecture : conception de structures complexes

Astuce mnémotechnique 🧠

Pour retenir l’effet des homothéties : « Rapport k, distances multipliées par |k|, volumes par |k| cube! ». Pour les rotations : « Cosinus et sinus, tournent en même temps! ».