Le théorème fondamental 📘

Le théorème des accroissements finis (TAF) est un résultat crucial qui relie la variation d’une fonction à sa dérivée.

Énoncé : Si f est continue sur [a,b] et dérivable sur ]a,b[, alors il existe c ∈ ]a,b[ tel que :

Interprétation géométrique 📊

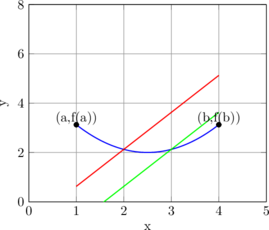
Le TAF assure qu’il existe au moins un point où la tangente est parallèle à la corde reliant (a, f(a)) à (b, f(b)).

Applications pratiques 🎯

1. Encadrement : Si on connaît un encadrement de f’, on peut encadrer f(b) – f(a)

2. Preuve d’inégalités : Montrer que sin x ≤ x pour x ≥ 0

3. Étude de suites : Méthode de point fixe

Exemple détaillé 🔍

Montrons que pour tout x > 0, 1/(1+x) < ln(1+1/x) < 1/x

Appliquons le TAF à f(t) = ln(t) sur [x, x+1] :

Il existe c ∈ ]x, x+1[ tel que f'(c) = [ln(x+1) – ln(x)]/1 = ln(1+1/x)

Or f'(c) = 1/c, et comme x < c < x+1, on a 1/(x+1) < 1/c < 1/x

Donc 1/(1+x) < ln(1+1/x) < 1/x

Cas particulier : Théorème de Rolle 🎲

Si f(a) = f(b), alors il existe c ∈ ]a,b[ tel que f'(c) = 0

C’est un cas particulier du TAF qui garantit l’existence d’un extremum ou d’un point d’inflexion.

Astuce mnémotechnique 💡

« TAF : Tangente Affine à la Fonction » ou « La pente moyenne existe quelque part ! »