🎯 Comprendre les suites récurrentes
Les suites définies par récurrence sont extrêmement importantes en mathématiques car elles modélisent de nombreux phénomènes réels où l’état suivant dépend de l’état précédent. 🔄
🧮 Structure générale
Une suite récurrente est définie par :
- Un terme initial : u₀ (ou u₁)
- Une relation de récurrence : uₙ₊₁ = f(uₙ)
Où f est une fonction qui permet de calculer le terme suivant à partir du terme courant.
📝 Types de suites récurrentes
1. Suites récurrentes linéaires d’ordre 1 📏
Ce sont les plus courantes : uₙ₊₁ = a×uₙ + b
Avec :
- a : coefficient multiplicatif
- b : terme constant
Exemple détaillé : u₀ = 1 et uₙ₊₁ = 0.5×uₙ + 2
Calculons les premiers termes :
- u₀ = 1
- u₁ = 0.5×1 + 2 = 2.5
- u₂ = 0.5×2.5 + 2 = 3.25
- u₃ = 0.5×3.25 + 2 = 3.625
- u₄ = 0.5×3.625 + 2 = 3.8125
2. Suites récurrentes non linéaires 🎢
La relation fait intervenir des opérations non linéaires comme des carrés, racines, etc.
Exemple : u₀ = 2 et uₙ₊₁ = √(uₙ + 1)
- u₀ = 2
- u₁ = √(2 + 1) = √3 ≈ 1.732
- u₂ = √(1.732 + 1) = √2.732 ≈ 1.653
- u₃ = √(1.653 + 1) = √2.653 ≈ 1.629
🔍 Méthode : Comment étudier une suite récurrente
Étape 1 : Calcul des premiers termes 🧮
On calcule toujours les 4-5 premiers termes pour se faire une idée du comportement.
Étape 2 : Recherche d’un point fixe 🎯
Un point fixe ℓ vérifie : ℓ = f(ℓ)
Pour uₙ₊₁ = 0.5×uₙ + 2, on résout :
![]()
![]()
![]()
![]()
Le point fixe est 4.
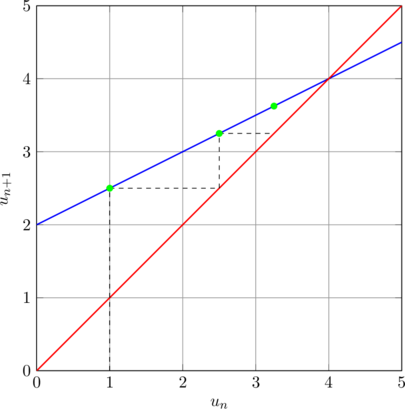
Étape 3 : Représentation graphique 📊
On peut visualiser l’évolution d’une suite récurrente avec la méthode de la toile d’araignée :
💡 Cas particuliers importants
Suite arithmétique récurrente
uₙ₊₁ = uₙ + r avec r constante
Exemple : u₀ = 3, uₙ₊₁ = uₙ + 2
- u₀ = 3
- u₁ = 3 + 2 = 5
- u₂ = 5 + 2 = 7
- u₃ = 7 + 2 = 9
Suite géométrique récurrente
uₙ₊₁ = q×uₙ avec q constante
Exemple : u₀ = 5, uₙ₊₁ = 0.5×uₙ
- u₀ = 5
- u₁ = 5×0.5 = 2.5
- u₂ = 2.5×0.5 = 1.25
- u₃ = 1.25×0.5 = 0.625
🔧 Méthode de résolution pratique
Pour uₙ₊₁ = a×uₙ + b
On peut trouver une formule explicite en utilisant le point fixe ℓ = b/(1-a) (si a ≠ 1) :
![]()
Application : u₀ = 1, uₙ₊₁ = 0.5×uₙ + 2
Point fixe : ℓ = 2/(1-0.5) = 4
Formule explicite : uₙ = 4 + (1-4)×0.5ⁿ = 4 – 3×0.5ⁿ
Vérification pour n=2 : u₂ = 4 – 3×0.25 = 4 – 0.75 = 3.25 ✓
🌍 Applications réelles
Modèle de population 🐇
Une population de lapins double chaque année, mais 100 individus sont prélevés :
Pₙ₊₁ = 2×Pₙ – 100
Avec P₀ = 200 lapins.
Dépression économique 📉
Un pays a un PIB qui baisse de 10% chaque année, mais reçoit 50 milliards d’aide :
PIBₙ₊₁ = 0.9×PIBₙ + 50
🧠 Technique mnémotechnique
« RÉCURRENCE = RÉPÉTITION » 🔁
Pour se souvenir qu’une suite récurrente se calcule terme à terme : « Comme un escalier, on monte marche par marche, en utilisant toujours la même règle pour passer à la marche suivante. » 🪜
Attention aux pièges : Bien vérifier à partir de quel indice la relation s’applique et ne pas confondre uₙ₊₁ et uₙ !

