Suites bornées 🎯
Une suite (uₙ) est dite bornée s’il existe un réel M > 0 tel que pour tout n ∈ ℕ, |uₙ| ≤ M.
On distingue :
- Suite majorée : ∃ M ∈ ℝ tel que ∀ n ∈ ℕ, uₙ ≤ M
- Suite minorée : ∃ m ∈ ℝ tel que ∀ n ∈ ℕ, uₙ ≥ m
- Suite bornée : à la fois majorée et minorée
Exemples 📝
La suite uₙ = (-1)ⁿ est bornée car ∀ n ∈ ℕ, |uₙ| = 1 ≤ 2
La suite uₙ = n² est minorée par 0 mais n’est pas majorée
Convergence des suites 🔍
Une suite (uₙ) converge vers un réel L si :
∀ ε > 0, ∃ N ∈ ℕ tel que ∀ n ≥ N, |uₙ – L| < ε
On note alors :
![]()
Si une suite ne converge vers aucun réel L, on dit qu’elle diverge.
Interprétation géométrique 📐
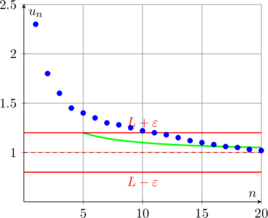
La convergence signifie qu’à partir d’un certain rang, tous les termes de la suite sont dans l’intervalle ]L-ε, L+ε[, aussi petit que soit ε.
Théorèmes importants sur la convergence 🎓
Théorème 1 : Toute suite convergente est bornée
Théorème 2 : Si une suite est croissante et majorée, alors elle converge
Théorème 3 : Si une suite est décroissante et minorée, alors elle converge
Théorème 4 (Unicité de la limite) : Si une suite converge, sa limite est unique
Exemple d’application 🧪
Étudions la suite définie par u₀ = 1 et uₙ₊₁ = √(2 + uₙ)
1. Montrons par récurrence que la suite est majorée par 2
2. Montrons qu’elle est croissante
3. Elle converge donc vers L qui vérifie L = √(2 + L)
En résolvant L² – L – 2 = 0, on trouve L = 2 (car L ≥ 0)
![]()
Astuce mnémotechnique 🧠
Pour retenir la définition de la convergence, pensez à « Pour tout epsilon strictement positif, il existe un naturel N tel que pour n plus grand que N, uₙ est epsilon-proche de L ». La précision s’améliore indéfiniment !

