Bienvenue dans cette dernière leçon où nous allons explorer les relations entre deux variables ! 🔗 Cette compétence est cruciale pour comprendre les liens qui peuvent exister entre différents phénomènes.
🔗 Introduction aux séries doubles
Jusqu’à présent, nous avons étudié une seule variable à la fois. Maintenant, nous allons examiner deux variables simultanément pour voir si elles sont liées.
Exemples de situations réelles :
- Le lien entre le budget publicitaire et les ventes
- La relation entre le temps d’étude et les notes
- La corrélation entre température et consommation d’énergie
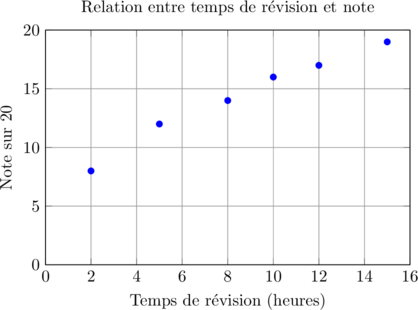
📊 Le nuage de points
C’est la représentation graphique fondamentale pour deux variables quantitatives. Chaque point représente un individu avec ses deux caractéristiques.
Prenons l’exemple d’une étude sur le lien entre le temps de révision et la note à un examen :
| Élève | Temps (h) | Note/20 |
|---|---|---|
| A | 2 | 8 |
| B | 5 | 12 |
| C | 8 | 14 |
| D | 10 | 16 |
| E | 12 | 17 |
| F | 15 | 19 |
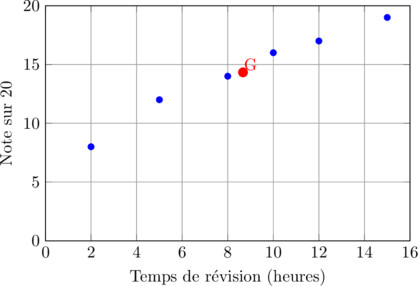
📈 Le point moyen
Le point moyen G a pour coordonnées les moyennes des deux variables :
![]()
Dans notre exemple :
![]()
![]()
Ajoutons ce point sur notre graphique :
📏 La covariance
La covariance mesure la façon dont deux variables varient ensemble :
![]()
Calculons-la pour notre exemple :
| xi | yi | xi-¯x | yi-¯y | Produit |
|---|---|---|---|---|
| 2 | 8 | -6,67 | -6,33 | 42,22 |
| 5 | 12 | -3,67 | -2,33 | 8,55 |
| 8 | 14 | -0,67 | -0,33 | 0,22 |
| 10 | 16 | 1,33 | 1,67 | 2,22 |
| 12 | 17 | 3,33 | 2,67 | 8,89 |
| 15 | 19 | 6,33 | 4,67 | 29,56 |
| Somme | 91,66 | |||
![]()
📊 Le coefficient de corrélation
Plus utile que la covariance, le coefficient de corrélation de Pearson est standardisé entre -1 et 1 :
![]()
Calculons d’abord les écarts-types :
![]()
![]()
Maintenant le coefficient :
![]()
Une valeur de 0,95 indique une corrélation positive très forte !
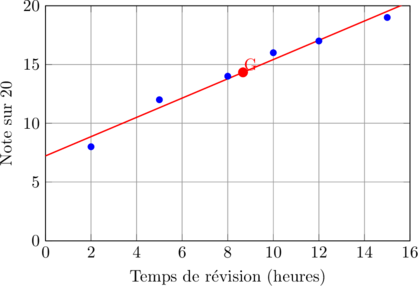
📐 La droite d’ajustement
Quand les points sont alignés, on peut tracer une droite d’ajustement. Son équation est :
![]()
Avec :
![]()
![]()
Dans notre exemple :
![]()
![]()
Donc : y = 0,82x + 7,22
Représentation graphique complète :
🎯 Interprétation et prédiction
Avec notre droite, on peut faire des prédictions ! Par exemple, pour 7 heures de révision :
![]()
On peut prédire une note d’environ 13/20.
Attention : Cette prédiction n’est valable que dans la plage de nos données observées.
⚠️ Les pièges à éviter
- Corrélation n’est pas causalité : Deux variables peuvent être corrélées sans qu’il y ait de lien de cause à effet
- Attention aux valeurs extrêmes : Un point aberrant peut fausser complètement l’analyse
- Vérifier la linéarité : La droite d’ajustement n’est valable que si les points sont alignés
💡 Astuce mnémotechnique
Pour interpréter le coefficient de corrélation :
- 0,8 à 1 : Corrélation forte
- 0,5 à 0,8 : Corrélation modérée
- 0 à 0,5 : Corrélation faible
- Négatif : Les variables varient en sens inverse
Félicitations ! 🎉 Tu maîtrises maintenant les concepts fondamentaux des statistiques à deux variables. Tu peux organiser, analyser et interpréter des données comme un véritable expert !

