Résolution d’équations logarithmiques et exponentielles 🧮
La résolution d’équations et d’inéquations faisant intervenir des logarithmes et des exponentielles repose sur leurs propriétés algébriques et leur réciprocité.
Équations exponentielles de base 🔢
Pour résoudre une équation de la forme aˣ = b :
- Si b > 0, alors x = ln(b)/ln(a)
- Si b ≤ 0, l’équation n’a pas de solution
Exemple : Résoudre 2ˣ = 8
2ˣ = 8 ⇔ 2ˣ = 2³ ⇔ x = 3
Ou en utilisant les logarithmes : x = ln(8)/ln(2) = 3
Équations logarithmiques de base 🔢
Pour résoudre une équation de la forme ln(x) = a :
ln(x) = a ⇔ x = eᵃ (avec x > 0)
Exemple : Résoudre ln(x) = 2
ln(x) = 2 ⇔ x = e² ≈ 7,389
Équations plus complexes 🎯
Exemple 1 : Résoudre e²ˣ – 3eˣ + 2 = 0
On pose X = eˣ, l’équation devient : X² – 3X + 2 = 0
Δ = 9 – 8 = 1, donc X = (3 ± 1)/2
X₁ = 2 et X₂ = 1
Ainsi, eˣ = 2 ⇒ x = ln(2) ou eˣ = 1 ⇒ x = 0
Les solutions sont x = 0 et x = ln(2)
Exemple 2 : Résoudre ln(x + 1) + ln(x – 1) = ln(3)
Conditions d’existence : x + 1 > 0 et x – 1 > 0 ⇒ x > 1
ln[(x + 1)(x – 1)] = ln(3) ⇒ ln(x² – 1) = ln(3)
x² – 1 = 3 ⇒ x² = 4 ⇒ x = 2 ou x = -2
Seule x = 2 est acceptable (car x > 1)
Inéquations exponentielles 📈
La fonction exponentielle étant strictement croissante :
![]()
Exemple : Résoudre e²ˣ > eˣ⁺¹
e²ˣ > eˣ⁺¹ ⇔ 2x > x + 1 ⇔ x > 1
Solution : x ∈ ]1, +∞[
Inéquations logarithmiques 📉
La fonction logarithme étant strictement croissante sur ]0, +∞[ :
![]()
Exemple : Résoudre ln(2x – 1) < ln(x + 3)
Conditions : 2x – 1 > 0 et x + 3 > 0 ⇒ x > 1/2
ln(2x – 1) < ln(x + 3) ⇔ 2x – 1 < x + 3 ⇔ x < 4
Solution : x ∈ ]1/2, 4[
Cas particuliers importants ⚠️
Inéquation avec changement de sens :
Pour 0 < a < 1, la fonction aˣ est décroissante :
![]()
Exemple : Résoudre (1/2)ˣ > (1/2)³
Comme 0 < 1/2 < 1, l'inéquation équivaut à x < 3
Méthodologie générale de résolution 📋
- Déterminer le domaine de définition (conditions d’existence)
- Simplifier l’équation/inéquation en utilisant les propriétés
- Se ramener à une forme simple (aˣ = b ou ln(x) = a)
- Résoudre l’équation/inéquation simple
- Vérifier que les solutions appartiennent au domaine
Problèmes concrets de modélisation 🌍
Problème 1 : Désintégration radioactive
La masse d’un élément radioactif suit la loi : m(t) = m₀ × e⁻ᵏᵗ
Si la demi-vie est de 10 ans, déterminer k.
Demi-vie : m(10) = m₀/2 ⇒ e⁻¹⁰ᵏ = 1/2
-10k = ln(1/2) = -ln(2) ⇒ k = ln(2)/10
Problème 2 : Croissance bactérienne
Une population double toutes les 3 heures. Combien de temps pour multiplier par 8 ?
N(t) = N₀ × 2ᵗᐟ³
On veut N(t) = 8N₀ ⇒ 2ᵗᐟ³ = 8 = 2³
t/3 = 3 ⇒ t = 9 heures
Représentation graphique des solutions 📊
Pour visualiser les solutions d’une inéquation comme eˣ > x + 1 :
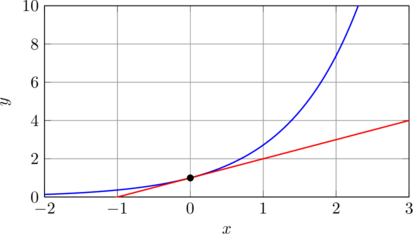
La solution de eˣ > x + 1 est x ∈ ]0, +∞[
Astuces de résolution 💡
- « Toujours vérifier les conditions d’existence avant de résoudre »
- « Pour les équations exponentielles complexes, penser au changement de variable X = eˣ »
- « Attention au sens des inégalités quand la base est entre 0 et 1 »

