Résolution d'équations complexes

Accueil » Leçons » Résolution d’équations complexes

Nombres complexes

Équations du premier degré 🔍

Une équation complexe du premier degré s’écrit az + b = 0, où a et b sont complexes et a ≠ 0.

La solution est : $z = -\frac{b}{a}$

Exemple :

Résoudre (1 + i)z + 2 – 3i = 0

Solution : $z = -\frac{2 - 3i}{1 + i}$

Multiplions numérateur et dénominateur par le conjugué du dénominateur :

$z = -\frac{(2 - 3i)(1 - i)}{(1 + i)(1 - i)} = -\frac{(2 - 3i)(1 - i)}{1^2 + 1^2} = -\frac{(2 - 3i)(1 - i)}{2}$

Développons le numérateur : (2 – 3i)(1 – i) = 2×1 – 2×i – 3i×1 + 3i×i = 2 – 2i – 3i + 3i² = 2 – 5i – 3 = -1 – 5i

Donc : $z = -\frac{-1 - 5i}{2} = \frac{1 + 5i}{2}$

Équations du second degré 🧩

Une équation du second degré à coefficients réels s’écrit az² + bz + c = 0, avec a ≠ 0.

Le discriminant est Δ = b² – 4ac.

Si Δ > 0 : deux solutions réelles
Si Δ = 0 : une solution réelle double
Si Δ < 0 : deux solutions complexes conjuguées

Les solutions sont : $z = \frac{-b \pm \sqrt{\Delta}}{2a}$

Exemple :

Résoudre z² – 4z + 13 = 0

Δ = (-4)² – 4×1×13 = 16 – 52 = -36

Donc : $z = \frac{4 \pm \sqrt{-36}}{2} = \frac{4 \pm 6i}{2} = 2 \pm 3i$

Équations polynomiales de degré n 🎓

Pour résoudre zⁿ = w où w est un complexe donné, on utilise la forme exponentielle.

Si $w = \lvert w \rvert e^{i\phi}$ , alors les solutions sont :

$z_k = \sqrt[n]{\lvert w \rvert} e^{i(\phi + 2k\pi)/n}$ pour k = 0, 1, 2, …, n-1

Exemple :

Résoudre z³ = 8i

Écrivons 8i sous forme exponentielle : |8i| = 8, arg(8i) = π/2

Donc : $8i = 8 e^{i\pi/2}$

Les solutions sont : $z_k = \sqrt[3]{8} e^{i(\pi/2 + 2k\pi)/3} = 2 e^{i(\pi/6 + 2k\pi/3)}$

Pour k = 0, 1, 2 :

$z_0 = 2 e^{i\pi/6} = 2(\cos(\pi/6) + i\sin(\pi/6)) = \sqrt{3} + i$

$z_1 = 2 e^{i5\pi/6} = 2(\cos(5\pi/6) + i\sin(5\pi/6)) = -\sqrt{3} + i$

$z_2 = 2 e^{i3\pi/2} = 2(\cos(3\pi/2) + i\sin(3\pi/2)) = -2i$

Représentation graphique des solutions 📊

Les solutions de zⁿ = w se situent sur un cercle de rayon $\sqrt[n]{\lvert w \rvert}$ et sont régulièrement espacées de $\frac{2\pi}{n}$ .

Pour l’exemple z³ = 8i :

Rendered by QuickLaTeX.com

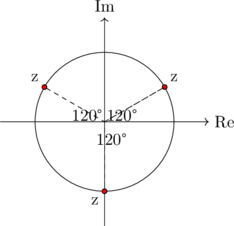
Équations avec conjugués 🔁

Pour résoudre des équations faisant intervenir le conjugué, on pose généralement z = x + iy et on sépare partie réelle et partie imaginaire.

Exemple :

Résoudre z + 2̅z = 3 + i

Posons z = x + iy, alors ̅z = x – iy

L’équation devient : (x + iy) + 2(x – iy) = 3 + i

⇒ x + iy + 2x – 2iy = 3 + i

⇒ (3x) + i(-y) = 3 + i

Par identification :

3x = 3 ⇒ x = 1

-y = 1 ⇒ y = -1

Donc z = 1 – i

Théorème fondamental de l’algèbre 📚

Tout polynôme à coefficients complexes de degré n admet exactement n racines complexes (comptées avec leur multiplicité).

Si les coefficients sont réels, alors les racines non réelles apparaissent par paires conjuguées.

Méthode générale de résolution 🛠️

Identifier le type d’équation (premier degré, second degré, zⁿ = w, etc.)
Choisir la méthode appropriée
Utiliser la forme la plus adaptée (algébrique, trigonométrique ou exponentielle)
Vérifier les solutions en les replaçant dans l’équation initiale
Interpréter géométriquement si possible

Astuce mnémotechnique 💡

Pour les équations du second degré : « Discriminant négatif = solutions conjuguées ». Pour zⁿ = w : « Les solutions sont sur un cercle et forment un polygone régulier ».