Le raisonnement par récurrence est une méthode de démonstration puissante qui permet de prouver qu’une propriété est vraie pour tous les entiers naturels. C’est comme une « cascade de dominos » : si le premier domino tombe, et que chaque domino fait tomber le suivant, alors tous les dominos tombent.
📋 Les trois étapes du raisonnement par récurrence
Étape 1 : Initialisation
On vérifie que la propriété est vraie au rang initial (généralement n=0 ou n=1).
Étape 2 : Hérédité
On suppose que la propriété est vraie à un rang n (c’est l’hypothèse de récurrence), et on démontre qu’elle est alors vraie au rang n+1.
Étape 3 : Conclusion
On conclut que la propriété est vraie pour tout entier naturel à partir du rang initial.
🔍 Exemple fondamental : la somme des n premiers entiers
Propriété à démontrer : Pour tout n ≥ 1, 1 + 2 + 3 + … + n = n(n+1)/2
Étape 1 : Initialisation (n=1)
Pour n=1 : 1 = 1×2/2 = 1 ✓
La propriété est vraie au rang 1.
Étape 2 : Hérédité
On suppose que pour un certain n ≥ 1, on a :
1 + 2 + … + n = n(n+1)/2 (hypothèse de récurrence)
On veut montrer que : 1 + 2 + … + n + (n+1) = (n+1)(n+2)/2
Démonstration :
1 + 2 + … + n + (n+1) = [n(n+1)/2] + (n+1) (d’après l’hypothèse)
= (n+1)[n/2 + 1] = (n+1)(n+2)/2 ✓
Étape 3 : Conclusion
La propriété est vraie pour tout n ≥ 1.
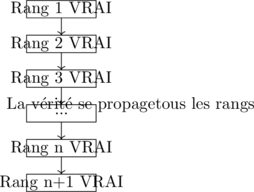
📊 Représentation visuelle du principe
Le raisonnement par récurrence peut être visualisé comme une cascade :
🎯 Application aux suites : exemple détaillé
Problème : Soit la suite définie par u₀ = 1 et uₙ₊₁ = 2uₙ + 1
Démontrer que pour tout n ∈ ℕ, uₙ = 2ⁿ⁺¹ – 1
Étape 1 : Initialisation (n=0)
Pour n=0 : u₀ = 1 et 2⁰⁺¹ – 1 = 2 – 1 = 1 ✓
Étape 2 : Hérédité
On suppose que pour un certain n, uₙ = 2ⁿ⁺¹ – 1
On veut montrer que uₙ₊₁ = 2⁽ⁿ⁺¹⁾⁺¹ – 1 = 2ⁿ⁺² – 1
D’après la définition : uₙ₊₁ = 2uₙ + 1
= 2(2ⁿ⁺¹ – 1) + 1 = 2ⁿ⁺² – 2 + 1 = 2ⁿ⁺² – 1 ✓
Étape 3 : Conclusion
La formule est vraie pour tout n ∈ ℕ.
🔍 Autre exemple : inégalité de Bernoulli
Propriété : Pour tout réel a ≥ -1 et tout n ∈ ℕ, (1 + a)ⁿ ≥ 1 + na
Étape 1 : Initialisation (n=0)
(1 + a)⁰ = 1 ≥ 1 + 0×a = 1 ✓
Étape 2 : Hérédité
On suppose (1 + a)ⁿ ≥ 1 + na
On veut montrer : (1 + a)ⁿ⁺¹ ≥ 1 + (n+1)a
(1 + a)ⁿ⁺¹ = (1 + a)ⁿ × (1 + a)
≥ (1 + na)(1 + a) (car 1 + a ≥ 0)
= 1 + a + na + na² = 1 + (n+1)a + na²
≥ 1 + (n+1)a (car na² ≥ 0) ✓
Étape 3 : Conclusion
L’inégalité est vraie pour tout n ∈ ℕ.
⚠️ Pièges à éviter
Piège 1 : Oublier l’initialisation
Si la propriété est fausse au rang initial, tout le raisonnement s’effondre.
Piège 2 : Mauvaise utilisation de l’hypothèse
L’hypothèse de récurrence ne s’applique qu’au rang n, pas à n+1.
Piège 3 : Récurrence forte
Parfois, on a besoin de supposer la propriété vraie pour tous les rangs ≤ n, pas seulement pour n.
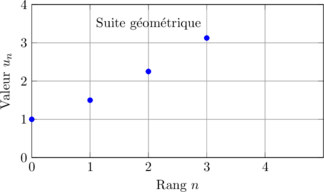
📈 Application graphique
Voici comment évolue une suite définie par récurrence :
💡 Astuce mnémotechnique
Pour retenir les trois étapes :
« I Like Heroes »
- I = Initialisation
- L = L’hypothèse (de récurrence)
- H = Hérédité
Et n’oubliez pas : « Sans initialisation, pas de récurrence ! »

