Propriétés des intégrales

Accueil » Leçons » Propriétés des intégrales

Primitives et intégrales

L’intégrale d’une fonction sur un intervalle [a,b] représente l’aire algébrique entre la courbe de la fonction et l’axe des abscisses. La notation est :

$\int_a^b f(x) dx$

📊 Propriétés fondamentales

1. Relation avec les primitives

Si F est une primitive de f sur [a,b], alors :

$\int_a^b f(x) dx = F(b) - F(a)$

C’est le théorème fondamental de l’analyse ! 🎉

Exemple : Calculer ∫₀¹ x² dx

Une primitive de x² est x³/3, donc :

$\int_0^1 x^2 dx = \left[ \frac{x^3}{3} \right]_0^1 = \frac{1^3}{3} - \frac{0^3}{3} = \frac{1}{3}$

2. Linéarité de l’intégrale

Pour toutes fonctions f et g et tout réel k :

$\int_a^b [f(x) + g(x)] dx = \int_a^b f(x) dx + \int_a^b g(x) dx$

$\int_a^b k f(x) dx = k \int_a^b f(x) dx$

3. Relation de Chasles

Pour tout c dans [a,b] :

$\int_a^b f(x) dx = \int_a^c f(x) dx + \int_c^b f(x) dx$

4. Positivité

Si f(x) ≥ 0 sur [a,b], alors :

$\int_a^b f(x) dx \geq 0$

🧮 Calculs pratiques

Exemple 1 : Calculer ∫₁² (3x² + 2x) dx

Primitive : F(x) = x³ + x²

$\int_1^2 (3x^2 + 2x) dx = [x^3 + x^2]_1^2 = (8 + 4) - (1 + 1) = 12 - 2 = 10$

Exemple 2 : Calculer ∫₀^π cos(x) dx

Primitive : F(x) = sin(x)

$\int_0^\pi \cos(x) dx = [\sin(x)]_0^\pi = \sin(\pi) - \sin(0) = 0 - 0 = 0$

📈 Interprétation géométrique

L’intégrale représente l’aire sous la courbe. Voici une illustration :

Rendered by QuickLaTeX.com

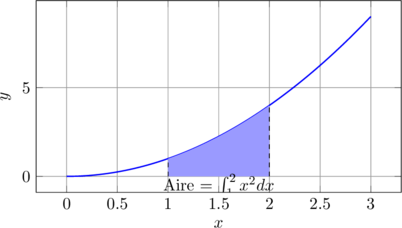
⚠️ Attention aux signes

Si la fonction est négative sur l’intervalle, l’intégrale donne une valeur négative. L’aire géométrique, elle, est toujours positive !

Exemple : ∫_0^π sin(x) dx

$\int_0^\pi \sin(x) dx = [-\cos(x)]_0^\pi = (-\cos(\pi)) - (-\cos(0)) = (1) - (-1) = 2$

💡 Valeur moyenne d’une fonction

La valeur moyenne de f sur [a,b] est :

$\frac{1}{b-a} \int_a^b f(x) dx$

Exemple : Valeur moyenne de f(x) = x² sur [0,2]

$\frac{1}{2-0} \int_0^2 x^2 dx = \frac{1}{2} \times \left[ \frac{x^3}{3} \right]_0^2 = \frac{1}{2} \times \frac{8}{3} = \frac{4}{3}$

🔍 Récapitulatif

Les intégrales permettent de calculer des aires et des valeurs moyennes. Le théorème fondamental relie intégrales et primitives. N’oubliez pas les propriétés de linéarité et la relation de Chasles !