📊 Introduction aux fonctions numériques

Une fonction numérique est une relation qui associe à chaque nombre réel x d’un ensemble de départ (appelé ensemble de définition) un unique nombre réel y. On note généralement :

Par exemple, la fonction f définie par f(x) = 2x + 3 associe à chaque nombre x son double augmenté de 3.

🧮 Vocabulaire essentiel

• Variable : la lettre x qui peut prendre différentes valeurs
• Image : la valeur f(x) correspondant à un x donné
• Antécédent : un nombre x dont l’image est f(x)
• Ensemble de définition : l’ensemble des valeurs que peut prendre x

📈 Représentation graphique

La courbe représentative d’une fonction f dans un repère est l’ensemble des points de coordonnées (x; f(x)). Chaque point de cette courbe a pour abscisse une valeur de x et pour ordonnée son image f(x).

Voici un exemple de courbe représentative :

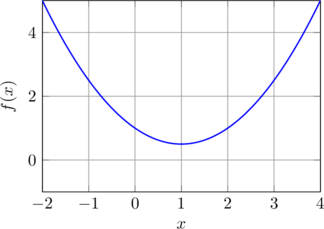
🔍 Lecture graphique d’images et d’antécédents

Pour trouver l’image d’un nombre a :

• Placer a sur l’axe des abscisses
• Remonter verticalement jusqu’à la courbe
• Se déplacer horizontalement vers l’axe des ordonnées
• Lire la valeur f(a)

Pour trouver les antécédents d’un nombre b :

• Placer b sur l’axe des ordonnées
• Se déplacer horizontalement jusqu’à la courbe
• Descendre verticalement vers l’axe des abscisses
• Lire les valeurs de x correspondantes

🎯 Exemple concret

Soit la fonction f(x) = x² – 4. Son ensemble de définition est ℝ (tous les nombres réels).

• L’image de 3 est : f(3) = 3² – 4 = 9 – 4 = 5
• Les antécédents de 0 sont les solutions de x² – 4 = 0, soit x = 2 et x = -2

💡 Astuce mnémotechnique

« Image = résultat = ordonnée » et « Antécédent = origine = abscisse ». Pensez à l’alphabet : A (Antécédent) vient avant I (Image), et A correspond à l’Abscisse !