Méthodes de résolution (substitution, combinaison)

Accueil » Leçons » Méthodes de résolution (substitution, combinaison)

Résolution de systèmes d’équations linéaires dans ℝ³

Maintenant que nous comprenons ce qu’est un système d’équations, découvrons comment le résoudre ! 🛠️ Nous allons explorer deux méthodes principales : la substitution et la combinaison.

Méthode de substitution 🔄

Cette méthode consiste à exprimer une inconnue en fonction des autres, puis à substituer cette expression dans les autres équations.

Étapes de la méthode de substitution :

Choisir une équation et une inconnue à exprimer
Exprimer cette inconnue en fonction des autres
Substituer cette expression dans les autres équations
Résoudre le système réduit à deux inconnues
Remonter pour trouver la troisième inconnue

Exemple détaillé 📝

Résolvons le système :

$\begin{cases} 2x + y - z = 5 \\ x - y + 2z = -1 \\ 3x + 2y + z = 8 \end{cases}$

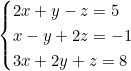
Étape 1 : Exprimons x en fonction de y et z à partir de la deuxième équation :

$x = y - 2z - 1$

Étape 2 : Substituons x dans les deux autres équations :

Première équation : 2(y – 2z – 1) + y – z = 5

$2y - 4z - 2 + y - z = 5$

$3y - 5z = 7$

Troisième équation : 3(y – 2z – 1) + 2y + z = 8

$3y - 6z - 3 + 2y + z = 8$

$5y - 5z = 11$

Nous obtenons un système à deux inconnues :

$\begin{cases} 3y - 5z = 7 \\ 5y - 5z = 11 \end{cases}$

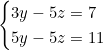
Étape 3 : Résolvons ce système. Soustraisons la première équation de la seconde :

$(5y - 5z) - (3y - 5z) = 11 - 7$

$2y = 4$

$y = 2$

Remplaçons y dans 3y – 5z = 7 :

$3(2) - 5z = 7$

$6 - 5z = 7$

$-5z = 1$

$z = -\frac{1}{5}$

Étape 4 : Trouvons x à partir de x = y – 2z – 1 :

$x = 2 - 2(-\frac{1}{5}) - 1$

$x = 2 + \frac{2}{5} - 1$

$x = 1 + \frac{2}{5} = \frac{7}{5}$

La solution est donc :

$x = \frac{7}{5}, \quad y = 2, \quad z = -\frac{1}{5}$

Méthode de combinaison (ou d’élimination) ➕➖

Cette méthode consiste à combiner les équations pour éliminer progressivement les inconnues.

Étapes de la méthode de combinaison :

Choisir une inconnue à éliminer
Combiner les équations deux à deux pour éliminer cette inconnue
Obtenir un système à deux inconnues
Résoudre ce système réduit
Remonter pour trouver la troisième inconnue

Exemple détaillé 📝

Reprenons le même système :

$\begin{cases} 2x + y - z = 5 \\ x - y + 2z = -1 \\ 3x + 2y + z = 8 \end{cases}$

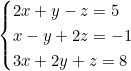
Étape 1 : Éliminons z. Ajoutons la première et la troisième équation :

$(2x + y - z) + (3x + 2y + z) = 5 + 8$

$5x + 3y = 13$

Multiplions la première équation par 2 et ajoutons-la à la seconde :

$2(2x + y - z) + (x - y + 2z) = 2\times5 + (-1)$

$4x + 2y - 2z + x - y + 2z = 10 - 1$

$5x + y = 9$

Nous obtenons le système :

$\begin{cases} 5x + 3y = 13 \\ 5x + y = 9 \end{cases}$

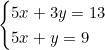
Étape 2 : Soustraisons la seconde équation de la première :

$(5x + 3y) - (5x + y) = 13 - 9$

$2y = 4$

$y = 2$

Étape 3 : Remplaçons y dans 5x + y = 9 :

$5x + 2 = 9$

$5x = 7$

$x = \frac{7}{5}$

Étape 4 : Trouvons z à partir de la première équation :

$2(\frac{7}{5}) + 2 - z = 5$

$\frac{14}{5} + 2 - z = 5$

$\frac{14}{5} + \frac{10}{5} - z = \frac{25}{5}$

$\frac{24}{5} - z = \frac{25}{5}$

$-z = \frac{1}{5}$

$z = -\frac{1}{5}$

Comparaison des méthodes 🔍

Substitution : Plus intuitive, mais peut devenir complexe avec des coefficients compliqués
Combinaison : Plus systématique, souvent plus rapide pour les systèmes simples

Cas particuliers ⚠️

Système incompatible :

$\begin{cases} x + y + z = 1 \\ 2x + 2y + 2z = 3 \\ x - y + z = 0 \end{cases}$

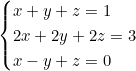
La deuxième équation est le double de la première, mais avec un second membre différent : contradiction !

Système indéterminé :

$\begin{cases} x + y + z = 1 \\ 2x + 2y + 2z = 2 \\ 3x + 3y + 3z = 3 \end{cases}$

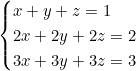
Toutes les équations sont proportionnelles : infinité de solutions !

Astuce mnémotechnique 💡

Pour choisir entre substitution et combinaison : « Substitution quand une inconnue est isolée, combinaison quand les coefficients sont simples » !

Récapitulatif

La substitution exprime une inconnue en fonction des autres
La combinaison élimine les inconnues par additions/soustractions
Les deux méthodes mènent au même résultat
Il faut savoir reconnaître les cas particuliers