🎯 Qu’est-ce qu’un système d’équations linéaires ?
Un système d’équations linéaires dans ℝ³ est un ensemble de plusieurs équations linéaires à trois inconnues, généralement notées x, y et z. Ces systèmes nous permettent de modéliser des situations où plusieurs conditions doivent être satisfaites simultanément. 📊
La forme générale d’un système de trois équations à trois inconnues est :
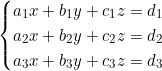
où les coefficients aᵢ, bᵢ, cᵢ et les constantes dᵢ sont des nombres réels.
🧮 Notations et terminologie
Il existe plusieurs façons de représenter un système linéaire :
- Forme développée : avec toutes les équations écrites explicitement
- Forme matricielle : plus compacte et élégante
- Forme vectorielle : mettant en évidence les combinaisons linéaires
La notation matricielle est particulièrement importante :
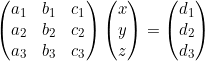
On appelle la première matrice la matrice des coefficients, le vecteur (x, y, z) est le vecteur inconnu, et le dernier vecteur est le vecteur constant.
🔍 Interprétation géométrique dans ℝ³
Chaque équation linéaire à trois inconnues représente un plan dans l’espace tridimensionnel. La solution du système correspond donc aux points d’intersection de ces plans. 📐
Il existe trois cas possibles :
- Solution unique : Les trois plans se coupent en un seul point
- Infinité de solutions : Les plans se coupent selon une droite ou coïncident
- Aucune solution : Les plans sont parallèles ou s’intersectent deux à deux sans point commun aux trois
Voici une représentation visuelle de ces différents cas :
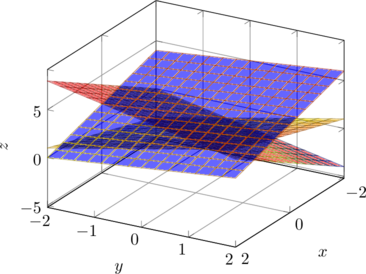
📝 Exemple concret
Imaginons que nous voulons déterminer les prix de trois fruits : pommes (x), bananes (y) et cerises (z). Nous avons les informations suivantes :
- 2 pommes + 3 bananes + 1 cerise coûtent 10€
- 1 pomme + 2 bananes + 3 cerises coûtent 15€
- 3 pommes + 1 banane + 2 cerises coûtent 12€
Ce problème se traduit par le système :
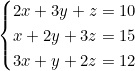
Nous apprendrons dans les prochaines leçons comment résoudre ce système !
💡 Astuce mnémotechnique
Pour retenir les différents types de solutions, pensez à l’analogie des « murs qui se rencontrent » :
- Trois murs qui se rejoignent dans un coin → solution unique
- Deux murs qui forment un angle → infinité de solutions le long de la ligne d’intersection
- Murs parallèles qui ne se rencontrent jamais → aucune solution

