Introduction aux systèmes d'équations à trois inconnues

Accueil » Leçons » Introduction aux systèmes d’équations à trois inconnues

Résolution de systèmes d’équations linéaires dans ℝ³

Bienvenue dans cette première leçon sur les systèmes d’équations linéaires à trois inconnues ! 🎯 Nous allons découvrir ensemble ce que sont ces systèmes et pourquoi ils sont si importants en mathématiques.

Qu’est-ce qu’un système d’équations linéaires à trois inconnues ?

Un système d’équations linéaires à trois inconnues est un ensemble de plusieurs équations où nous cherchons les valeurs de trois variables (généralement notées x, y et z) qui vérifient simultanément toutes les équations du système.

La forme générale d’un tel système est :

$\begin{cases} a_1x + b_1y + c_1z = d_1 \\ a_2x + b_2y + c_2z = d_2 \\ a_3x + b_3y + c_3z = d_3 \end{cases}$

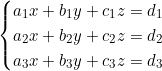
où a₁, a₂, a₃, b₁, b₂, b₃, c₁, c₂, c₃, d₁, d₂, d₃ sont des nombres réels appelés coefficients.

Exemple concret 🌟

Imaginons que tu veuilles acheter des fruits : des pommes (x), des bananes (y) et des oranges (z). Tu as les informations suivantes :

2 pommes + 3 bananes + 1 orange coûtent 10€
1 pomme + 2 bananes + 3 oranges coûtent 15€
3 pommes + 1 banane + 2 oranges coûtent 12€

Ce problème se traduit par le système :

$\begin{cases} 2x + 3y + z = 10 \\ x + 2y + 3z = 15 \\ 3x + y + 2z = 12 \end{cases}$

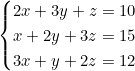
Terminologie importante 📚

Voici quelques termes que tu rencontreras souvent :

Inconnues : les variables x, y, z que nous cherchons à déterminer
Coefficients : les nombres qui multiplient les inconnues
Second membre : les nombres à droite du signe égal
Solution : le triplet (x, y, z) qui vérifie toutes les équations

Représentation matricielle

Pour faciliter la résolution, on peut représenter le système sous forme matricielle :

$\begin{pmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{pmatrix} \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} d_1 \\ d_2 \\ d_3 \end{pmatrix}$

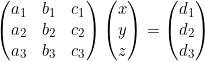
Types de systèmes

Il existe trois types de systèmes possibles :

Système compatible déterminé : une solution unique ✨
Système compatible indéterminé : une infinité de solutions 🔄
Système incompatible : aucune solution ❌

Exemple de système compatible déterminé

$\begin{cases} x + y + z = 6 \\ 2x - y + z = 3 \\ x + 2y - z = 2 \end{cases}$

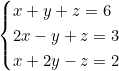
Ce système a une solution unique : x = 1, y = 2, z = 3

Astuce mnémotechnique 💡

Pour retenir la structure d’un système à trois inconnues, pense à « 3 équations, 3 inconnues, 3 dimensions ». Chaque équation représente un plan dans l’espace, et la solution est le point d’intersection de ces trois plans !

Récapitulatif

Un système d’équations linéaires relie trois inconnues par plusieurs équations
La solution est le triplet (x, y, z) qui vérifie toutes les équations
Il existe trois types de systèmes selon le nombre de solutions
La représentation matricielle facilite la résolution