Qu’est-ce qu’une équation différentielle ? 🤔
Une équation différentielle est une équation qui relie une fonction inconnue à ses dérivées. Elle exprime comment la variation d’une grandeur (représentée par la dérivée) dépend de la grandeur elle-même.
En Terminale S, nous étudions principalement les équations différentielles du premier ordre, qui ne font intervenir que la fonction et sa dérivée première.
La forme générale d’une équation différentielle du premier ordre est :
![]()
où y est la fonction inconnue et y’ sa dérivée.
À quoi servent les équations différentielles ? 🎯
Les équations différentielles sont omniprésentes en sciences pour modéliser des phénomènes d’évolution :
- Physique : mouvement, circuits électriques, radioactivité
- Biologie : croissance de populations, diffusion de maladies
- Économie : modèles de croissance, évolution des marchés
- Chimie : cinétique des réactions
Notion de condition initiale 🧭
Une équation différentielle admet généralement une infinité de solutions. Pour sélectionner une solution particulière, on impose une condition initiale, c’est-à-dire la valeur de la fonction en un point donné.
Par exemple, si on connaît la position initiale d’un mobile, on peut déterminer sa trajectoire exacte.
Exemple fondamental : la croissance exponentielle 📈
Un des modèles les plus simples est celui de la croissance exponentielle, décrit par l’équation :
![]()
où k est une constante réelle. Cette équation exprime que la vitesse de croissance est proportionnelle à la quantité présente.
Les solutions de cette équation sont de la forme :
![]()
où C est une constante déterminée par la condition initiale.
Représentation graphique 📊
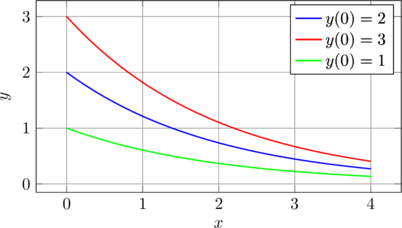
Les solutions d’une équation différentielle forment une famille de courbes. Chaque condition initiale sélectionne une courbe particulière.
Voici une représentation de plusieurs solutions de l’équation y’ = -0.5y :
Récapitulatif mnémotechnique 🧠
Pour retenir l’essentiel : Équation Différentielle = Relation entre une fonction et son taux de variation. Pensez à « ED » comme « Évolution Dynamique » !

