La fonction exponentielle 🚀
La fonction exponentielle, notée exp(x) ou ex, est l’unique fonction égale à sa dérivée et valant 1 en 0.
![]()
![]()
![]()
Propriétés fondamentales 🔑
• e0 = 1
• ex > 0 pour tout x réel
• limx→+∞ ex = +∞
• limx→-∞ ex = 0
La fonction logarithme népérien 📝
Le logarithme népérien, noté ln(x), est la fonction réciproque de l’exponentielle :
![]()
![]()
Propriétés algébriques 🧮
![]()
![]()
![]()
Représentation graphique 📈
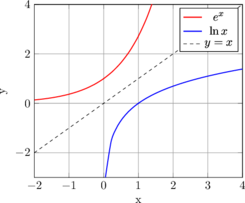
Les courbes de ex et ln(x) sont symétriques par rapport à la droite y = x.
Résolution d’équations 🔍
Exemple : Résoudre e2x – 3ex + 2 = 0
On pose X = ex, l’équation devient X² – 3X + 2 = 0
Solutions : X = 1 ou X = 2
Donc ex = 1 ⇒ x = 0 ou ex = 2 ⇒ x = ln(2)
Astuce 💡
Pour retenir les propriétés : « L’exponentielle transforme les sommes en produits, le logarithme fait l’inverse ! »

