La fonction logarithme naturel, notée ln, est l’une des fonctions les plus importantes en mathématiques. Elle est définie comme la réciproque de la fonction exponentielle de base e.

La fonction logarithme népérien est définie pour tout nombre réel strictement positif x > 0. Sa définition formelle est :

Propriétés fondamentales 🔑

Le logarithme naturel possède plusieurs propriétés algébriques essentielles :

• Logarithme d’un produit : ln(ab) = ln(a) + ln(b)
• Logarithme d’un quotient : ln(a/b) = ln(a) – ln(b)
• Logarithme d’une puissance : ln(aⁿ) = n × ln(a)
• Logarithme de 1 : ln(1) = 0
• Logarithme de e : ln(e) = 1

Ces propriétés sont fondamentales pour simplifier les expressions logarithmiques.

Représentation graphique 📊

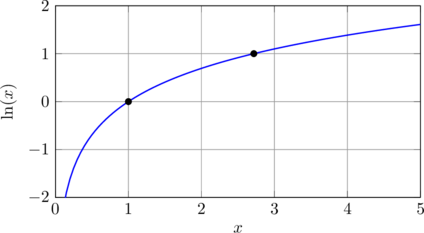
La courbe représentative de la fonction ln a les caractéristiques suivantes :

• Elle est définie uniquement pour x > 0
• Elle passe par le point (1, 0)
• Elle passe par le point (e, 1)
• Elle est strictement croissante sur ]0, +∞[
• Elle admet l’axe des ordonnées comme asymptote verticale

Exemples de calcul 🔢

Exemple 1 : Calculer ln(e³)

D’après la propriété des puissances : ln(e³) = 3 × ln(e) = 3 × 1 = 3

Exemple 2 : Simplifier ln(8) – ln(2)

ln(8) – ln(2) = ln(8/2) = ln(4)

Comme 4 = 2², on a ln(4) = 2 × ln(2)

Exemple 3 : Résoudre ln(x) = 2

ln(x) = 2 ⇔ x = e² ≈ 7,389

Dérivée de la fonction ln 📐

La dérivée de la fonction logarithme naturel est une propriété fondamentale :

Cette formule est valable pour tout x > 0. La dérivée montre que la pente de la tangente à la courbe en un point x est exactement 1/x.

Application pratique : échelle logarithmique 🎯

Les logarithmes sont utilisés dans de nombreuses échelles de mesure :

• Échelle de Richter pour les séismes
• Décibels pour l’intensité sonore
• pH pour l’acidité des solutions

Par exemple, un séisme de magnitude 6 est 10 fois plus puissant qu’un séisme de magnitude 5 sur l’échelle de Richter.

Astuce mnémotechnique 💡

Pour retenir les propriétés du logarithme : « Les logarithmes transforment les produits en sommes, les quotients en différences, et les puissances en produits. »