📈 L’importance de l’étude des variations
L’étude des variations d’une fonction permet de connaître son comportement : où elle croît, où elle décroît, et où elle atteint ses extremums. C’est essentiel pour tracer sa courbe représentative avec précision. ✨
🔗 Rappel sur la dérivée
La dérivée f'(x) mesure le taux de variation instantané de la fonction. Son signe nous renseigne sur les variations :
- Si f'(x) > 0 → f est croissante
- Si f'(x) < 0 → f est décroissante
- Si f'(x) = 0 → extremum possible
📝 Méthodologie complète
Pour étudier les variations d’une fonction :
- Calculer la dérivée f'(x)
- Déterminer le signe de f'(x)
- Établir le tableau de variations
- Identifier les extremums
🧮 Exemple détaillé
Soit la fonction f(x) = x³ – 3x² + 2
Étape 1 : Calcul de la dérivée
![]()
Étape 2 : Signe de la dérivée
f'(x) = 3x(x – 2)
Racines : x = 0 et x = 2
Tableau de signes :
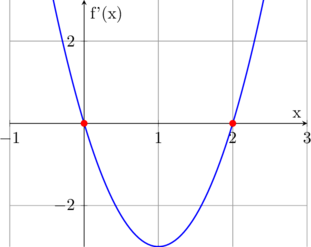
Étape 3 : Tableau de variations
| x | -∞ | 0 | 2 | +∞ | |
|---|---|---|---|---|---|
| f'(x) | + | 0 | – | 0 | + |
| f(x) | ↗ | Max | ↘ | Min | ↗ |
Étape 4 : Calcul des extremums
f(0) = 2 → maximum local
f(2) = -2 → minimum local
🎯 Cas particuliers
Fonctions rationnelles : Attention aux valeurs interdites dans le domaine !
Fonctions trigonométriques : Périodicité à prendre en compte.
Fonctions exponentielles : Toujours strictement monotones.
💡 Astuce pratique
Pour vérifier votre tableau de variations, calculez quelques valeurs particulières :
- Les limites aux bornes du domaine
- Les images des racines de la dérivée
- Quelques points intermédiaires
Récapitulatif : La dérivée est votre meilleur allié pour comprendre comment une fonction « se comporte » ! 📊

