📐 Introduction à la notion de dérivée
La dérivée d’une fonction en un point mesure le taux de variation instantané de cette fonction, c’est-à-dire la pente de la tangente à sa courbe en ce point. C’est un outil fondamental pour étudier les variations d’une fonction. 🎢
🧮 Définition mathématique
La dérivée de f en un point a est définie par la limite :
![]()
Quand cette limite existe, on dit que la fonction est dérivable en a.
📚 Dérivées des fonctions usuelles
Voici les dérivées des fonctions de référence qu’il faut absolument connaître :
| Fonction f(x) | Dérivée f'(x) |
|---|---|
| k (constante) | 0 |
| x | 1 |
| x² | 2x |
| xⁿ (n ∈ ℝ) | nxⁿ⁻¹ |
| √x | 1/(2√x) |
| 1/x | -1/x² |
🔧 Règles de dérivation
Pour dériver des fonctions plus complexes, on utilise des règles opératoires :
- Somme : (u + v)’ = u’ + v’
- Produit par une constante : (k × u)’ = k × u’
- Produit : (u × v)’ = u’v + uv’
- Quotient : (u/v)’ = (u’v – uv’)/v²
🎯 Exemples détaillés
Exemple 1 : Dériver f(x) = 3x² + 5x – 2
On applique les règles :
- Dérivée de 3x² : 3 × 2x = 6x
- Dérivée de 5x : 5 × 1 = 5
- Dérivée de -2 : 0
Donc : f'(x) = 6x + 5
Exemple 2 : Dériver g(x) = 4√x + 7/x
- Dérivée de 4√x : 4 × (1/(2√x)) = 2/√x
- Dérivée de 7/x : 7 × (-1/x²) = -7/x²
Donc : g'(x) = 2/√x – 7/x²
📊 Interprétation graphique
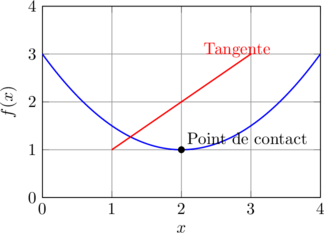
La dérivée f'(a) représente le coefficient directeur de la tangente à la courbe au point d’abscisse a. Plus cette valeur est grande (en valeur absolue), plus la courbe est « pentue » en ce point.
💡 Mémo dérivation
« Puissance descend, constante reste, racine devient fraction ! » Pour xⁿ, la puissance n « descend » en multiplicateur et devient n-1.

