Datation et énergie nucléaire

Accueil » Leçons » Datation et énergie nucléaire

Radioactivité et applications nucléaires

La datation radioactive ⏳

La datation radioactive utilise la décroissance naturelle des isotopes radioactifs pour déterminer l’âge d’objets ou de matériaux.

Principe de la datation au carbone 14

Le carbone 14 est produit dans l’atmosphère et absorbé par les êtres vivants. À leur mort, l’absorption cesse et le carbone 14 se désintègre.

$\^{14}_6C \rightarrow \^{14}_7N + e^- + \bar\nu_e$

Période radioactive : T = 5730 ans

Formule de datation

L’âge t d’un échantillon se calcule par :

$t = \frac{T}{\ln 2} \ln\left(\frac{N_0}{N(t)}\right)$

Exemple pratique : Un échantillon contient 25% du carbone 14 initial. Quel est son âge ?

$t = \frac{5730}{\ln 2} \ln\left(\frac{1}{0.25}\right) = \frac{5730}{0.693} \times \ln(4) = 8268 \times 1.386 = 11460 \text{ ans}$

Énergie de liaison nucléaire 💥

L’énergie de liaison Eₗ est l’énergie qu’il faut fournir pour séparer un noyau en ses nucléons individuels.

$E_l = [Zm_p + (A-Z)m_n - m_{noyau}]c^2$

Où :

Z : nombre de protons
A : nombre de masse
mₚ : masse du proton
mₙ : masse du neutron
mₙₒᵧₐᵤ : masse du noyau
c : vitesse de la lumière

Énergie de liaison par nucléon

L’énergie de liaison par nucléon est un indicateur de stabilité :

$\frac{E_l}{A} = \frac{[Zm_p + (A-Z)m_n - m_{noyau}]c^2}{A}$

Plus cette valeur est élevée, plus le noyau est stable.

Courbe d’Aston

Rendered by QuickLaTeX.com

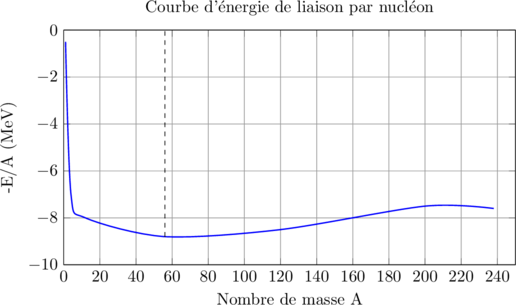
La fission nucléaire ⚛️

La fission est la division d’un noyau lourd en noyaux plus légers, avec libération d’énergie.

Exemple avec l’uranium 235 :

$\^{235}_{92}U + {}^1_0n \rightarrow \^{141}_{56}Ba + \^{92}_{36}Kr + 3{}^1_0n + \text{énergie}$

L’énergie libérée se calcule par le défaut de masse :

$\Delta E = \Delta m c^2$

La fusion nucléaire ☀️

La fusion est la combinaison de noyaux légers pour former un noyau plus lourd.

Exemple avec la fusion de deutérium et tritium :

$\^{2}_1H + {}^3_1H \rightarrow {}^4_2He + {}^1_0n + 17.6 \text{ MeV}$

Calcul d’énergie libérée

Problème : Calculer l’énergie libérée par la fission d’un noyau d’uranium 235.

Données : m(U-235) = 235.0439 u, m(Ba-141) = 140.9144 u, m(Kr-92) = 91.9262 u, m(n) = 1.0087 u

$\Delta m = [235.0439 + 1.0087] - [140.9144 + 91.9262 + 3\times1.0087]$

$\Delta m = 236.0526 - 235.8667 = 0.1859 \text{ u}$

$\Delta E = 0.1859 \times 931.5 = 173.2 \text{ MeV}$

Applications énergétiques

Les centrales nucléaires utilisent la fission contrôlée pour produire de l’électricité. 1 kg d’uranium 235 libère autant d’énergie que 3000 tonnes de charbon !

Récapitulatif 🔄

Datation : utiliser N(t) = N₀e^(-λt) avec la bonne période

Énergie : E = Δmc², toujours vérifier l’équilibre des masses

Fission : gros noyau → petits noyaux + neutrons + énergie

Fusion : petits noyaux → gros noyau + énergie