🎨 Tracer la courbe représentative

Le tracé de la courbe représentative est l’aboutissement de toute l’étude d’une fonction. C’est une synthèse visuelle qui permet de comprendre rapidement le comportement de la fonction. 🖼️

📋 Checklist avant le tracé

Avant de commencer, assurez-vous d’avoir :

• Le domaine de définition
• Les limites aux bornes
• Les asymptotes
• Le tableau de variations
• Quelques points particuliers

🔄 Méthode de tracé pas à pas

Étape 1 : Préparer le repère

Choisissez une échelle adaptée et placez les asymptotes en pointillés.

Étape 2 : Placer les points remarquables

Les extremums, intersections avec les axes, points d’inflexion.

Étape 3 : Tracer selon les variations

Respectez scrupuleusement le tableau de variations.

Étape 4 : Vérifier la cohérence

Assurez-vous que la courbe respecte les asymptotes.

📊 Exemple complet

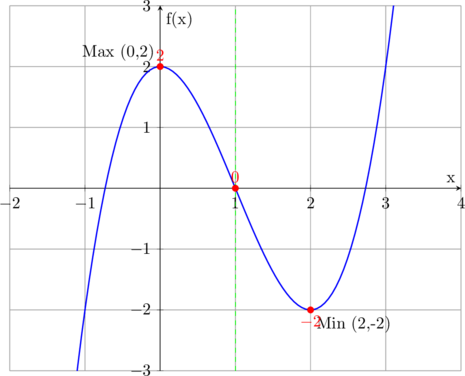
Reprenons f(x) = x³ – 3x² + 2

Points clés :

• Intersection avec Oy : (0,2)
• Intersections avec Ox : résoudre x³ – 3x² + 2 = 0
• Maximum : (0,2)
• Minimum : (2,-2)

Courbe représentative :

🎯 Points d’inflexion

Un point d’inflexion est où la courbe change de concavité. Pour le trouver, étudiez le signe de la dérivée seconde :

Pour notre exemple : f »(x) = 6x – 6

f »(x) = 0 quand x = 1 → point d’inflexion en (1,0)

🔍 Analyse fine du tracé

Concavité :

• f »(x) > 0 → concavité vers le haut
• f »(x) < 0 → concavité vers le bas

Tangentes : La pente de la tangente en un point est f'(x).

💪 Application pratique

Exercice guidé : Tracez la courbe de f(x) = (x²-1)/(x+2)

Domaines : ℝ{-2}

Asymptote verticale : x = -2

Asymptote oblique : y = x – 2

Tableau de variations à établir…

🌟 Conseils de pro

Pour un tracé réussi :

• Commencez toujours par les asymptotes
• Placez les points importants avec précision
• Suivez les variations avec régularité
• Vérifiez la cohérence globale

Astuce mnémotechnique : « Asymptotes d’abord, points ensuite, variations toujours ! » 🎯

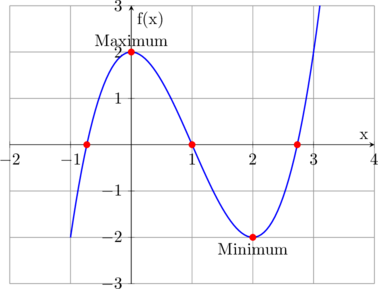
Voici le graphique complet de notre exemple avec tous les éléments :