La convergence est une notion fondamentale en analyse. Une suite converge vers une limite L si ses termes se rapprochent de plus en plus de L lorsque n devient très grand.
Définition formelle : Une suite (uₙ) converge vers L si :
∀ε > 0, ∃N ∈ ℕ tel que ∀n ≥ N, |uₙ – L| < ε
En d’autres termes : « Quelle que soit la précision ε que l’on choisit, à partir d’un certain rang N, tous les termes de la suite sont à une distance inférieure à ε de L ».
📈 Suites convergentes vs divergentes
Suite convergente : Possède une limite finie L
Suite divergente : Soit elle tend vers l’infini, soit elle n’a pas de limite
Types de divergence :
- Divergence vers +∞ : lim uₙ = +∞
- Divergence vers -∞ : lim uₙ = -∞
- Divergence oscillante : pas de limite
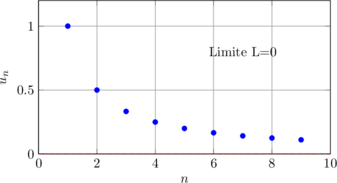
Exemple convergent : uₙ = 1/n
lim uₙ = 0 lorsque n → +∞
🔍 Méthodes pour étudier la convergence
Méthode 1 : Utilisation des limites usuelles
Limites à connaître :
![]()
![]()
![]()
Méthode 2 : Théorème des gendarmes
Si vₙ ≤ uₙ ≤ wₙ et si lim vₙ = lim wₙ = L, alors lim uₙ = L
Exemple : uₙ = sin(n)/n
On sait que -1 ≤ sin(n) ≤ 1, donc -1/n ≤ uₙ ≤ 1/n
Comme lim (-1/n) = 0 et lim (1/n) = 0, par le théorème des gendarmes, lim uₙ = 0
📊 Représentation des différents types de convergence
Convergence monotone :
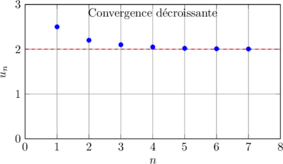
Divergence vers +∞ :
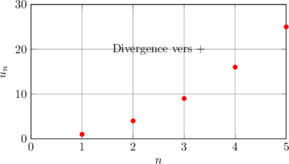
🎯 Théorèmes importants sur la convergence
Théorème 1 : Toute suite croissante et majorée converge
Théorème 2 : Toute suite décroissante et minorée converge
Théorème 3 : Toute suite convergente est bornée
Attention : La réciproque est fausse ! Une suite bornée n’est pas nécessairement convergente.
Contre-exemple : uₙ = (-1)ⁿ
Cette suite est bornée (-1 ≤ uₙ ≤ 1) mais diverge car elle oscille entre -1 et 1.
🔍 Exemple détaillé d’étude de convergence
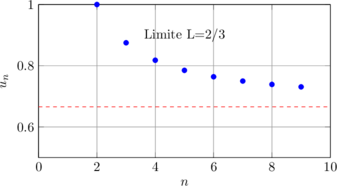
Étudier la suite : uₙ = (2n + 1)/(3n – 1)
Étape 1 : On factorise par les termes dominants
uₙ = n(2 + 1/n) / [n(3 – 1/n)] = (2 + 1/n)/(3 – 1/n)
Étape 2 : On passe à la limite
lim uₙ = lim (2 + 1/n)/(3 – 1/n) = 2/3
Étape 3 : Conclusion
La suite converge vers 2/3
💡 Astuce mnémotechnique
Pour retenir la définition de la convergence :
« ε pour Erreur, N pour Numéro – À partir du rang N, l’erreur est plus petite que ε »

