Concepts de base et vocabulaire des probabilités

Accueil » Leçons » Concepts de base et vocabulaire des probabilités

Probabilités fondamentales

Bienvenue dans cette première leçon sur les probabilités fondamentales ! 🎯 Nous allons découvrir ensemble les concepts de base qui te permettront de comprendre et de résoudre tes premiers problèmes de probabilités.

Les probabilités sont partout autour de nous : quand on parle de chances de gagner à un jeu, de probabilité qu’il pleuve demain, ou encore de risques dans la vie quotidienne. C’est une branche des mathématiques qui étudie les phénomènes aléatoires.

📚 Le vocabulaire essentiel

Expérience aléatoire : C’est une expérience dont on ne peut pas prédire le résultat à l’avance, mais dont on connaît tous les résultats possibles.

Exemple : Lancer un dé équilibré à 6 faces.

Univers (noté $\Omega$ ) : C’est l’ensemble de tous les résultats possibles d’une expérience aléatoire.

Exemple : Pour un dé à 6 faces, $\Omega = \{1, 2, 3, 4, 5, 6\}$

Événement : C’est un sous-ensemble de l’univers, c’est-à-dire un ou plusieurs résultats possibles.

Exemple : « Obtenir un nombre pair » est un événement qui correspond à $\{2, 4, 6\}$

Événement élémentaire : C’est un événement qui ne contient qu’un seul résultat.

Exemple : « Obtenir le nombre 3 » est un événement élémentaire.

🎲 La probabilité d’un événement

La probabilité d’un événement A, notée $P(A)$ , est un nombre compris entre 0 et 1 qui mesure la chance que cet événement se produise.

Propriétés fondamentales :

$0 \leq P(A) \leq 1$
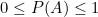
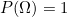$P(\Omega) = 1$ (la probabilité de l’univers est 1)
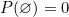$P(\varnothing) = 0$ (la probabilité de l’ensemble vide est 0)

Dans le cas d’une situation d’équiprobabilité (tous les résultats ont la même chance de se produire), on utilise la formule :

$P(A) = \frac{\text{nombre de cas favorables}}{\text{nombre de cas possibles}}$

Exemple : Pour un dé équilibré, la probabilité d’obtenir un nombre pair est :

Cas favorables : 2, 4, 6 (3 cas)

Cas possibles : 1, 2, 3, 4, 5, 6 (6 cas)

$P(\text{pair}) = \frac{3}{6} = \frac{1}{2} = 0,5$

🔍 Les événements particuliers

Événement certain : Événement qui se produit toujours ( $P = 1$ )

Événement impossible : Événement qui ne se produit jamais ( $P = 0$ )

Événements incompatibles : Deux événements qui ne peuvent pas se produire en même temps.

Astuce mnémotechnique : Pense à un dé – « obtenir 1 » et « obtenir 2 » sont incompatibles, mais « obtenir un nombre pair » et « obtenir un multiple de 3 » sont compatibles (le 6 vérifie les deux).

🎉 Récapitulatif : Tu connais maintenant le vocabulaire de base des probabilités ! Retiens bien : univers, événement, probabilité, et la formule dans le cas équiprobable. Ces concepts sont les fondations de tout ce que nous verrons ensuite.