Le coefficient de corrélation est une mesure statistique qui quantifie l’intensité et le sens de la relation linéaire entre deux variables quantitatives. Il nous indique à quel point les variables évoluent ensemble.
Définition du coefficient de corrélation linéaire
Le coefficient de corrélation linéaire de Pearson, noté r, varie entre -1 et +1 :
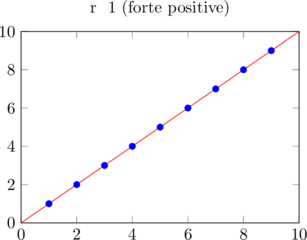
- r = +1 : corrélation positive parfaite
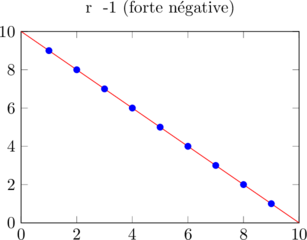
- r = -1 : corrélation négative parfaite
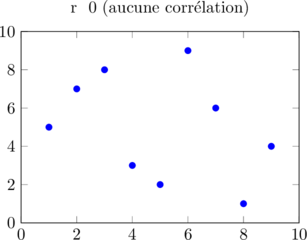
- r = 0 : absence de corrélation linéaire
Calcul du coefficient r 🧮
Formule de Pearson
Le coefficient de corrélation se calcule avec la formule :
![]()
Cette formule peut sembler complexe, mais elle se décompose en étapes simples.
Exemple détaillé 📋
Reprenons nos données sur les heures d’étude et les notes :
| Heures (x) | Note (y) | x-ẍ | y-ȳ | (x-ẍ)(y-ȳ) | (x-ẍ)² | (y-ȳ)² |
|---|---|---|---|---|---|---|
| 2 | 8 | -4 | -5,6 | 22,4 | 16 | 31,36 |
| 4 | 12 | -2 | -1,6 | 3,2 | 4 | 2,56 |
| 6 | 14 | 0 | 0,4 | 0 | 0 | 0,16 |
| 8 | 16 | 2 | 2,4 | 4,8 | 4 | 5,76 |
| 10 | 18 | 4 | 4,4 | 17,6 | 16 | 19,36 |
| Total | 48 | 40 | 59,2 |
Étape 1 : Calcul de la covariance
![]()
Étape 2 : Calcul des écarts-types
![]()
![]()
Étape 3 : Calcul de r
![]()
Nous obtenons un coefficient de corrélation très proche de 1, indiquant une forte corrélation positive.
Interprétation des valeurs de r 🔍
Échelle d’interprétation
- 0,9 ≤ |r| ≤ 1,0 : corrélation très forte
- 0,7 ≤ |r| < 0,9 : corrélation forte
- 0,5 ≤ |r| < 0,7 : corrélation modérée
- 0,3 ≤ |r| < 0,5 : corrélation faible
- 0,0 ≤ |r| < 0,3 : corrélation très faible ou nulle
Signification du signe
Le signe de r indique le sens de la relation :
- r > 0 : les variables varient dans le même sens
- r < 0 : les variables varient en sens opposé
Représentations graphiques selon r 📊
Voici différents nuages de points selon la valeur de r :
Corrélation vs causalité ⚠️
Attention aux interprétations abusives !
Une erreur fréquente est de confondre corrélation et causalité :
- Corrélation : les variables varient ensemble
- Causalité : une variable cause la variation de l’autre
Exemple classique 🍦
Il existe une forte corrélation positive entre les ventes de glaces et le nombre de noyades. Cela ne signifie pas que manger des glaces cause des noyades ! Les deux phénomènes sont causés par une troisième variable : la chaleur estivale.
Coefficient de détermination R² 📐
Définition et calcul
Le coefficient de détermination R² est le carré du coefficient de corrélation :
![]()
Dans notre exemple :
![]()
Interprétation de R²
R² représente la proportion de variance de y expliquée par x. Dans notre cas, 97% de la variation des notes est expliquée par le temps d’étude.
C’est un indicateur très utile pour évaluer la qualité d’un modèle de régression.
Applications pratiques 🌍
Domaines d’utilisation
- Recherche médicale : relation entre traitement et guérison
- Finance : corrélation entre actions
- Météorologie : relation température/vent
- Éducation : corrélation présence/réussite
Cas d’étude en psychologie 🧠
Une étude cherche à déterminer s’il existe une corrélation entre le temps passé sur les réseaux sociaux et le niveau de stress.
Données collectées :
- r = 0,72 (corrélation forte positive)
- R² = 0,52 (52% de la variance du stress expliquée)
Interprétation : il existe une relation significative, mais d’autres facteurs influencent aussi le stress.
Limites et précautions 🚨
Points importants à retenir
- La corrélation ne prouve pas la causalité
- Elle mesure seulement les relations linéaires
- Elle est sensible aux valeurs aberrantes
- La taille de l’échantillon influence la significativité
Test de significativité
Pour des échantillons de taille n, on peut tester si r est significativement différent de 0. En général, pour n ≥ 30, un |r| ≥ 0,35 est considéré comme significatif.
Récapitulatif mnémotechnique 🧠
r = +1 : parfaitement aligné ↗️
r = -1 : parfaitement opposé ↘️
r = 0 : pas de relation linéaire ➡️
R² = part expliquée de la variance
Pensez à r comme rapport et R² comme Rendement du modèle !

