Calculs et applications pratiques

Accueil » Leçons » Calculs et applications pratiques

Probabilités

🎯 Applications concrètes des probabilités

Les probabilités ne se limitent pas aux exercices théoriques ! Elles ont des applications dans de nombreux domaines de la vie quotidienne et professionnelle. 🌍

📈 Probabilités conditionnelles

Une probabilité conditionnelle mesure la probabilité qu’un événement se produise sachant qu’un autre événement est déjà réalisé.

Notation : P(A|B) se lit « probabilité de A sachant B »

Formule fondamentale :

$P(A|B) = \frac{P(A \cap B)}{P(B)}$

à condition que P(B) ≠ 0.

🔍 Exemple : Test médical

Un test de dépistage a les caractéristiques suivantes :

Sensibilité : P(test + | malade) = 0,95
Spécificité : P(test – | non malade) = 0,98
Prévalence : P(malade) = 0,01

Calculons P(malade | test +) :

$P(\text{malade}|+) = \frac{P(+|\text{malade}) \times P(\text{malade})}{P(+)}$

Avec P(+) = P(+|malade)×P(malade) + P(+|non malade)×P(non malade)

P(+) = 0,95×0,01 + 0,02×0,99 = 0,0095 + 0,0198 = 0,0293

Donc P(malade|+) = 0,0095/0,0293 ≈ 0,324

🎲 Loi des grands nombres

Cette loi fondamentale stipule que plus on répète une expérience aléatoire, plus la fréquence observée se rapproche de la probabilité théorique.

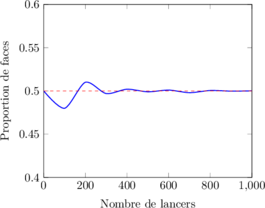
Si on lance une pièce équilibrée un très grand nombre de fois, la proportion de faces tend vers 0,5.

📊 Simulation avec graphique

Rendered by QuickLaTeX.com

🔢 Applications industrielles

Contrôle qualité : Dans une usine, 2% des pièces sont défectueuses. On prélève 50 pièces au hasard. Quelle est la probabilité d’avoir au plus 1 pièce défectueuse ?

X ∼ B(50; 0,02)

P(X ≤ 1) = P(X = 0) + P(X = 1)

$P(X = 0) = \binom{50}{0} \times (0,02)^0 \times (0,98)^{50} \approx 0,364$

$P(X = 1) = \binom{50}{1} \times (0,02)^1 \times (0,98)^{49} \approx 0,372$

P(X ≤ 1) ≈ 0,364 + 0,372 = 0,736

💼 Applications financières

Évaluation de risque : Une banque estime que 3% de ses clients risquent de ne pas rembourser un prêt. Elle accorde 100 prêts.

X ∼ B(100; 0,03) représente le nombre de défauts.

Espérance : E(X) = 100 × 0,03 = 3 défauts

Probabilité d’avoir plus de 5 défauts :

P(X > 5) = 1 – P(X ≤ 5) ≈ 1 – 0,916 = 0,084

🎯 Problème combinatoire avancé

Problème : On dispose de 10 cartes numérotées de 1 à 10. On tire 3 cartes simultanément. Quelle est la probabilité que la somme des numéros soit supérieure à 20 ?

Solution :

Nombre total de tirages :

$\binom{10}{3} = 120$

Combinaisons donnant une somme > 20 :

{8,9,10} : somme = 27
{7,9,10} : somme = 26
{7,8,10} : somme = 25
{7,8,9} : somme = 24
{6,9,10} : somme = 25
{6,8,10} : somme = 24
{6,8,9} : somme = 23
{6,7,10} : somme = 23
{5,9,10} : somme = 24
{5,8,10} : somme = 23

Soit 10 combinaisons favorables.

Probabilité = 10/120 ≈ 0,0833

📈 Approximation de la loi binomiale

Lorsque n est grand et p pas trop proche de 0 ou 1, on peut approximer la loi binomiale par une loi normale :

Conditions : n ≥ 30, np ≥ 5, n(1-p) ≥ 5

Alors :

$X \sim \mathcal{B}(n, p) \approx \mathcal{N}(np, \sqrt{np(1-p)})$

🔍 Méthodologie de résolution

Pour résoudre un problème de probabilités :

Identifier l’expérience aléatoire
Définir les événements et la variable aléatoire
Vérifier les conditions d’application
Choisir la loi appropriée
Calculer avec précision
Interpréter le résultat dans le contexte

🌟 Conseils pratiques

Vérifiez toujours les hypothèses : indépendance, équiprobabilité, etc.

Utilisez des schémas : arbres, diagrammes pour visualiser

Interprétez les résultats : une probabilité de 0,05 signifie « 1 chance sur 20 »

🎯 Synthèse du cours

Vous maîtrisez maintenant :

Les concepts fondamentaux des probabilités
La loi binomiale et ses applications
Les méthodes de calcul et d’interprétation

Ces outils vous seront précieux dans de nombreux domaines ! 🚀