Applications pratiques

Accueil » Leçons » Applications pratiques

Équations différentielles

Modélisation de la décroissance radioactive ☢️

La loi de décroissance radioactive est un excellent exemple d’application des équations différentielles.

Soit N(t) le nombre de noyaux radioactifs à l’instant t. La vitesse de désintégration est proportionnelle au nombre de noyaux présents :

$\frac{dN}{dt} = - \lambda N$

où λ est la constante radioactive (caractéristique de l’élément).

Cette équation est à variables séparables :

$\frac{dN}{N} = - \lambda dt$

En intégrant :

$\int \frac{dN}{N} = - \lambda \int dt$

$\ln N = - \lambda t + C$

$N(t) = e^C e^{-\lambda t}$

Avec la condition initiale N(0) = N₀, on obtient :

$N(t) = N_0 e^{-\lambda t}$

La demi-vie t₁/₂ est le temps au bout duquel la moitié des noyaux se sont désintégrés :

$N(t_{1/2}) = \frac{N_0}{2} = N_0 e^{-\lambda t_{1/2}}$

d’où :

$t_{1/2} = \frac{\ln 2}{\lambda}$

Circuit RC électrique ⚡

Dans un circuit RC série, la tension $u_C$ aux bornes du condensateur vérifie :

$RC \frac{du_C}{dt} + u_C = E$

où R est la résistance, C la capacitance, et E la force électromotrice du générateur.

Cette équation peut se réécrire :

$\frac{du_C}{dt} = \frac{1}{RC} (E - u_C)$

C’est une équation à variables séparables. Sa solution est :

$u_C(t) = E (1 - e^{-t/(RC)})$

La constante τ = RC est appelée constante de temps du circuit.

Chute libre avec frottements 🍃

Pour un objet en chute verticale avec frottement fluide, la vitesse v vérifie :

$m \frac{dv}{dt} = mg - kv$

où m est la masse, g l’accélération de la pesanteur, et k un coefficient de frottement.

Cette équation devient :

$\frac{dv}{dt} = g - \frac{k}{m} v$

La solution est :

$v(t) = \frac{mg}{k} (1 - e^{-(k/m)t})$

La vitesse tend vers une vitesse limite $v_lim = mg/k$ .

Représentation graphique des modèles 📈

Comparaison de la décroissance radioactive pour deux éléments différents :

Rendered by QuickLaTeX.com

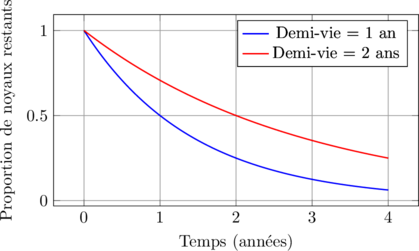
Charge du condensateur dans un circuit RC

Rendered by QuickLaTeX.com

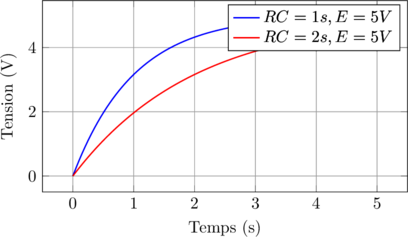
Conclusion et perspectives 🎓

Les équations différentielles sont des outils puissants pour modéliser des phénomènes d’évolution dans de nombreux domaines scientifiques. La méthode de séparation des variables permet de résoudre une large classe de problèmes concrets.

Pour aller plus loin, vous étudierez en classes préparatoires ou à l’université des équations différentielles plus complexes (ordre supérieur, coefficients variables, systèmes différentiels).

Mémo pratique 🧠

ED + Condition Initiale = Solution Unique. Gardez en tête que derrière chaque équation différentielle se cache un phénomène physique fascinant !