Applications des intégrales

Accueil » Leçons » Applications des intégrales

Primitives et intégrales

Les intégrales ne servent pas seulement à calculer des aires ! Elles ont de nombreuses applications pratiques dans divers domaines. Voyons les principales. 🚀

📐 Calcul d’aires planes

Aire entre deux courbes

L’aire entre les courbes y = f(x) et y = g(x) sur [a,b] est :

$A = \int_a^b |f(x) - g(x)| dx$

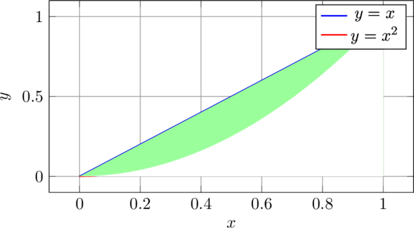
Exemple : Aire entre y = x² et y = x sur [0,1]

Sur [0,1], x ≥ x², donc :

$A = \int_0^1 (x - x^2) dx = \left[ \frac{x^2}{2} - \frac{x^3}{3} \right]_0^1 = \frac{1}{2} - \frac{1}{3} = \frac{1}{6}$

Représentation graphique

Rendered by QuickLaTeX.com

📊 Calcul de volumes

Volume de révolution

Le volume engendré par la rotation de la courbe y = f(x) autour de l’axe des abscisses sur [a,b] est :

$V = \pi \int_a^b [f(x)]^2 dx$

Exemple : Volume de la sphère de rayon R

On fait tourner le demi-cercle y = √(R² – x²) autour de l’axe Ox :

$V = \pi \int_{-R}^R (R^2 - x^2) dx = \pi \left[ R^2x - \frac{x^3}{3} \right]_{-R}^R = \frac{4}{3}\pi R^3$

⚖️ Applications physiques

Calcul de travail

Le travail d’une force variable F(x) sur un déplacement de a à b est :

$W = \int_a^b F(x) dx$

Exemple : Travail pour étirer un ressort

Si la force est F(x) = kx (loi de Hooke), le travail pour étirer de 0 à L est :

$W = \int_0^L kx dx = k \left[ \frac{x^2}{2} \right]_0^L = \frac{1}{2} k L^2$

Calcul de centres de gravité

Le centre de gravité d’une plaque plane a pour abscisse :

$x_G = \frac{\int_a^b x f(x) dx}{\int_a^b f(x) dx}$

💰 Applications économiques

Surplus du consommateur</h3

Le surplus mesure l’avantage que retirent les consommateurs :

$S = \int_0^{Q_0} [p_d(Q) - p_0] dQ$

où p_d(Q) est la fonction de demande et p₀ le prix d’équilibre.

🌡️ Applications biologiques

Croissance d’une population

Si le taux de croissance est r(t), la population totale sur une période est :

$P = \int_{t_1}^{t_2} r(t) dt$

📈 Exemple complet : Projet concret

Problème : Une entreprise veut calculer le bénéfice total sur 5 ans. Le bénéfice marginal (dérivée du bénéfice) est B'(t) = 50t – t² (en milliers d’euros par an).

Solution : Le bénéfice total sur 5 ans est :

$B = \int_0^5 (50t - t^2) dt = \left[ 25t^2 - \frac{t^3}{3} \right]_0^5$

$B = 25 \times 25 - \frac{125}{3} = 625 - 41.67 = 583.33$

Le bénéfice total est donc de 583 330 € 💰

🔍 Méthodologie de résolution

Pour résoudre un problème d’intégration :

Identifier la grandeur à calculer
Exprimer un élément infinitésimal
Intégrer sur l’intervalle approprié
Calculer l’intégrale
Interpréter le résultat

💡 Astuces pratiques

Pour les aires entre courbes, déterminer d’abord quelle fonction est au-dessus
Vérifier les unités dans les applications physiques
Penser à la signification géométrique pour interpréter les résultats

🎓 Récapitulatif final

Les intégrales sont des outils puissants pour résoudre des problèmes concrets : calcul d’aires, volumes, travail, bénéfices, etc. La clé est de bien comprendre le lien entre la grandeur cherchée et son expression infinitésimale. 🏆

N’oubliez pas : Pratiquez régulièrement pour maîtriser ces techniques !