🎯 Introduction à la notion de limite
La limite d’une suite décrit son comportement quand n devient très grand (tend vers l’infini). C’est un concept fondamental pour comprendre l’évolution à long terme des suites. 🎢
Quand on dit « n tend vers l’infini », on imagine que n prend des valeurs de plus en plus grandes : 100, 1000, 1000000… et on observe vers quelle valeur uₙ se rapproche.
📈 Les différents types de limites
1. Suite convergente 🎯
Une suite converge vers un nombre réel ℓ si les termes uₙ se rapprochent de plus en plus de ℓ quand n augmente.
Notation : ![]()
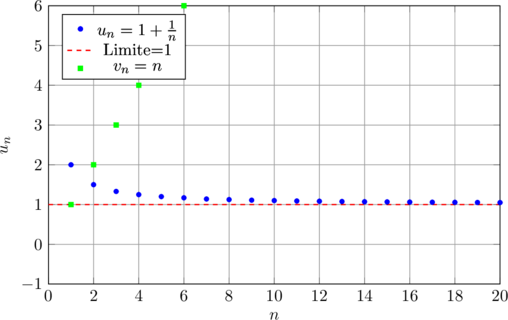
Exemple : uₙ = 1 + 1/n
- u₁ = 2
- u₁₀ = 1.1
- u₁₀₀ = 1.01
- u₁₀₀₀ = 1.001
La suite converge vers 1.
2. Suite divergente vers +∞ 🚀
Une suite diverge vers +∞ si les termes uₙ deviennent arbitrairement grands.
Notation : ![]()
Exemple : uₙ = n²
- u₁₀ = 100
- u₁₀₀ = 10000
- u₁₀₀₀ = 1000000
3. Suite divergente vers -∞ 📉
Une suite diverge vers -∞ si les termes uₙ deviennent arbitrairement petits (négatifs avec de grandes valeurs absolues).
Exemple : uₙ = -n
4. Suite qui ne possède pas de limite 🎭
Certaines suites n’ont pas de limite, comme uₙ = (-1)ⁿ qui alterne entre -1 et 1.
🔍 Méthodes pour déterminer une limite
Méthode 1 : Observation des premiers termes 👀
On calcule quelques termes pour se faire une intuition :
uₙ = (2n+1)/(n+3)
- u₁₀ = 21/13 ≈ 1.615
- u₁₀₀ = 201/103 ≈ 1.951
- u₁₀₀₀ = 2001/1003 ≈ 1.995
- La suite semble converger vers 2
Méthode 2 : Transformation algébrique 🧮
Pour uₙ = (2n+1)/(n+3), on factorise par n au numérateur et dénominateur :
![]()
Quand n → +∞, 1/n → 0 et 3/n → 0, donc :
![]()
📊 Représentation graphique des limites
Voici différents comportements de suites :
🎯 Règles de calcul des limites
Limites des suites usuelles
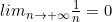

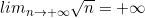
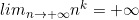 (pour k > 0)
(pour k > 0)
Opérations sur les limites
Si ![]() et
et ![]() :
:
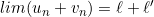
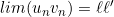
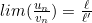 (si ℓ’ ≠ 0)
(si ℓ’ ≠ 0)
💡 Cas particuliers importants
Limite des suites géométriques
Pour uₙ = qⁿ :
- Si |q| < 1, alors
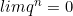
- Si q = 1, alors
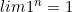
- Si q > 1, alors
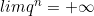
- Si q ≤ -1, la suite n’a pas de limite
Théorème des gendarmes 🚔
Si pour tout n, vₙ ≤ uₙ ≤ wₙ et si vₙ et wₙ convergent vers la même limite ℓ, alors uₙ converge aussi vers ℓ.
Exemple : uₙ = sin(n)/n
On a -1/n ≤ uₙ ≤ 1/n et ±1/n → 0, donc uₙ → 0.
🌍 Applications concrètes des limites
Dosage médicamenteux 💊
Un patient prend 200mg d’un médicament chaque jour. Son corps élimine 30% du médicament présent chaque jour.
Modèle : Mₙ₊₁ = 0.7×Mₙ + 200
Point fixe : ℓ = 200/(1-0.7) ≈ 666.67 mg
La concentration tend vers environ 667 mg.
Apprentissage 📚
Le nombre de mots qu’un étudiant peut mémoriser suit uₙ₊₁ = 0.8×uₙ + 50.
Limite : ℓ = 50/(1-0.8) = 250 mots
🧠 Règles mnémotechniques
« PETIT SUR GRAND TEND VERS ZÉRO » ➗
Quand le numérateur est borné et le dénominateur tend vers l’infini, la limite est 0.
« QUAND C’EST COMPLIQUÉ, FACTORISE PAR LE PLUS GRAND TERME » 🎯
Pour les fractions rationnelles, on factorise toujours par la plus grande puissance de n.
⚠️ Pièges à éviter
- Ne pas conclure trop vite en regardant seulement les premiers termes
- Vérifier les conditions d’application des théorèmes
- Attention aux formes indéterminées : ∞-∞, 0×∞, ∞/∞, 0/0
La notion de limite est fondamentale pour comprendre le comportement à long terme des suites et modéliser de nombreux phénomènes réels ! 🌟

