📊 Lien fondamental entre dérivée et courbe
La dérivée d’une fonction nous renseigne précieusement sur l’allure de sa courbe représentative. C’est un outil puissant pour étudier les variations d’une fonction sans avoir à calculer toutes ses valeurs. 🎯
📈 Variations et signe de la dérivée
Il existe une relation fondamentale entre le signe de la dérivée et les variations de la fonction :
- Si f'(x) > 0 sur un intervalle, alors f est strictement croissante sur cet intervalle ↗️
- Si f'(x) < 0 sur un intervalle, alors f est strictement décroissante sur cet intervalle ↘️
- Si f'(x) = 0 en un point, alors la tangente est horizontale en ce point ↔️
🎢 Extremums locaux
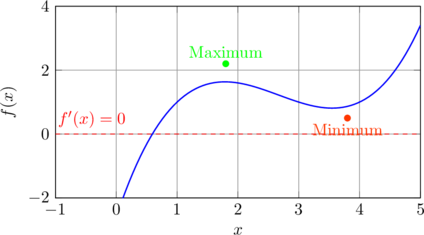
Un extremum local (maximum ou minimum) se produit aux points où la dérivée s’annule en changeant de signe :
- Maximum local : la dérivée passe de positive à négative
- Minimum local : la dérivée passe de négative à positive
🔍 Tableau de variation
Le tableau de variation synthétise toutes les informations sur les variations d’une fonction :
| x | -∞ | 1 | 3 | +∞ | |||
|---|---|---|---|---|---|---|---|
| f'(x) | + | 0 | – | 0 | + | ||
| f(x) | -∞ | ↗ | 4 | ↘ | -2 | ↗ | +∞ |
🎯 Exemple complet d’étude
Étudions la fonction f(x) = x³ – 3x² + 2 :
1. Calcul de la dérivée : f'(x) = 3x² – 6x = 3x(x – 2)
2. Signe de la dérivée :
- f'(x) = 0 pour x = 0 et x = 2
- f'(x) > 0 sur ]-∞; 0[ ∪ ]2; +∞[
- f'(x) < 0 sur ]0; 2[
3. Variations :
- Croissante sur ]-∞; 0] et [2; +∞[
- Décroissante sur [0; 2]
4. Extremums :
- Maximum local en x = 0 : f(0) = 2
- Minimum local en x = 2 : f(2) = -2
📐 Tangentes et interprétation géométrique
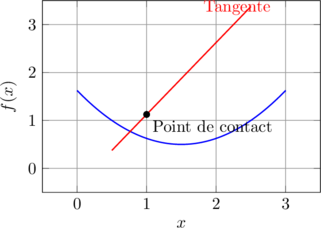
L’équation de la tangente à la courbe au point d’abscisse a est :
![]()
Cette droite « épouse » localement la courbe et sa pente nous indique la direction de croissance.
💡 Conseil pratique
« La dérivée est le GPS de la fonction : elle te dit où ça monte, où ça descend, et où faire une pause ! » Utilise toujours le signe de la dérivée pour prévoir les variations avant même de tracer la courbe.

