Découvrons maintenant la beauté géométrique des systèmes d’équations ! 🌌 Chaque équation linéaire à trois inconnues représente un plan dans l’espace, et la solution correspond à l’intersection de ces plans.
Représentation géométrique d’une équation 📐
Une équation de la forme ax + by + cz = d représente un plan dans l’espace ℝ³. Le vecteur (a, b, c) est normal à ce plan (il est perpendiculaire au plan).
Exemple : l’équation x + y + z = 1 représente un plan qui coupe les axes en (1,0,0), (0,1,0) et (0,0,1).
Interprétation géométrique d’un système
Un système de trois équations représente trois plans dans l’espace. La nature de la solution dépend de la position relative de ces trois plans.
Cas 1 : Solution unique (système compatible déterminé) ✨
Les trois plans se coupent en un seul point. C’est le cas général et le plus fréquent.
Exemple :
![\[\begin{cases} x + y + z = 6 \\ 2x - y + z = 3 \\ x + 2y - z = 2 \end{cases}\]](https://kilasy.com/wp-content/ql-cache/quicklatex.com-ab63afd263cf612c4a0f7cd02248e166_l3.png "Rendered by QuickLaTeX.com")
Ces trois plans se coupent au point (1, 2, 3).
Représentation schématique simplifiée :
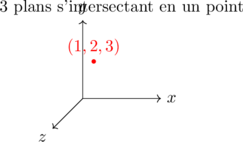
Cas 2 : Aucune solution (système incompatible) ❌
Les trois plans n’ont aucun point commun. Plusieurs configurations sont possibles :
- Deux plans parallèles distincts
- Trois plans formant un prisme
- Deux plans confondus et le troisième parallèle
Exemple de plans parallèles :
![\[\begin{cases} x + y + z = 1 \\ x + y + z = 2 \\ 2x - y + z = 0 \end{cases}\]](https://kilasy.com/wp-content/ql-cache/quicklatex.com-ddcb4f0704f2db7162d5ed59aea52a96_l3.png "Rendered by QuickLaTeX.com")
Les deux premiers plans sont parallèles mais distincts.
Cas 3 : Infinité de solutions (système compatible indéterminé) 🔄
Les trois plans ont une intersection commune qui est une droite ou un plan.
Sous-cas 3A : Intersection en une droite
Les trois plans se coupent selon une même droite.
Sous-cas 3B : Intersection en un plan
Les trois plans sont confondus.
Comment reconnaître géométriquement le type de solution ?
Examinons les vecteurs normaux des plans. Soient n₁, n₂, n₃ les vecteurs normaux des trois plans.
Cas 1 : Solution unique
Les trois vecteurs normaux sont linéairement indépendants.
![\[\det\begin{pmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{pmatrix} \neq 0\]](https://kilasy.com/wp-content/ql-cache/quicklatex.com-9a99af091f2e4e2e9cf4dd6685325e53_l3.png "Rendered by QuickLaTeX.com")
Cas 2 : Aucune solution
Au moins deux plans sont parallèles et distincts.
Cas 3 : Infinité de solutions
Les vecteurs normaux sont linéairement dépendants.
Représentation simplifiée des différents cas
Solution unique :
Aucune solution :
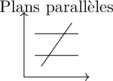
Infinité de solutions :
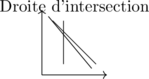
Application à des problèmes réels 🌍
- Problème de localisation : Déterminer sa position à partir de distances à trois points
- Problème de dosage : Trouver les concentrations de trois substances en chimie
Astuce mnémotechnique 💡
« Un point, une droite, ou rien du tout – la géométrie révèle le résultat partout ! »
Récapitulatif
- Chaque équation représente un plan dans ℝ³
- Solution unique = intersection en un point
- Aucune solution = pas de point commun
- Infinité de solutions = intersection en une droite ou un plan
- Les vecteurs normaux permettent de prévoir le type de solution