Régression linéaire

Accueil » Leçons » Régression linéaire

Statistiques descriptives

La régression linéaire est une méthode statistique qui permet d’étudier la relation entre deux variables quantitatives. Elle vise à trouver la droite qui représente le mieux la relation entre ces variables.

Le concept de corrélation linéaire

Avant de parler de régression, il faut comprendre qu’une relation linéaire existe lorsque les points d’un nuage semblent s’aligner selon une droite. Plus l’alignement est net, plus la relation est forte.

Équation de la droite de régression

La droite de régression linéaire a pour équation :

$y = ax + b$

Où :

y est la variable expliquée (dépendante)
x est la variable explicative (indépendante)
a est le coefficient directeur (pente)
b est l’ordonnée à l’origine

Calcul des coefficients a et b 🧮

Méthode des moindres carrés

La méthode la plus utilisée pour déterminer a et b est la méthode des moindres carrés, qui minimise la somme des carrés des écarts entre les points observés et la droite.

Formules de calcul

Le coefficient directeur a se calcule par :

$a = \frac{\sum{(x_i - \bar{x})(y_i - \bar{y})}}{\sum{(x_i - \bar{x})^2}}$

L’ordonnée à l’origine b se calcule par :

$b = \bar{y} - a\bar{x}$

Où $\bar{x}$ et $\bar{y}$ sont les moyennes respectives de x et y.

Exemple détaillé 📊

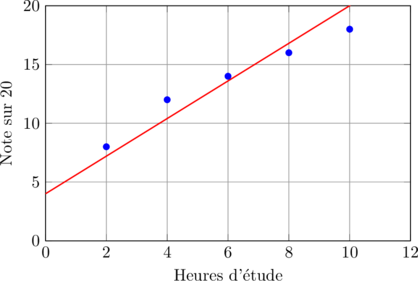
Considérons les données suivantes sur les heures d’étude et les notes obtenues :

Heures d’étude (x)	Note sur 20 (y)
2	8
4	12
6	14
8	16
10	18

Étape 1 : Calcul des moyennes

$\bar{x} = \frac{2+4+6+8+10}{5} = 6$

$\bar{y} = \frac{8+12+14+16+18}{5} = 13,6$

Étape 2 : Calcul des écarts

Nous calculons d’abord le numérateur et le dénominateur de la formule de a :

$\sum{(x_i - \bar{x})(y_i - \bar{y})} = (2-6)(8-13,6) + (4-6)(12-13,6) + \cdots = 64$

$\sum{(x_i - \bar{x})^2} = (2-6)^2 + (4-6)^2 + \cdots = 40$

Étape 3 : Calcul de a et b

$a = \frac{64}{40} = 1,6$

$b = 13,6 - 1,6 \times 6 = 4$

L’équation de la droite de régression est donc :

$y = 1,6x + 4$

Représentation graphique 📉

Voici le nuage de points et la droite de régression correspondante :

Rendered by QuickLaTeX.com

Interprétation des résultats 🔍

Signification du coefficient a

Le coefficient a = 1,6 signifie qu’en moyenne, chaque heure d’étude supplémentaire permet d’augmenter la note de 1,6 point.

Signification du coefficient b

Le coefficient b = 4 représente la note théorique qu’un étudiant obtiendrait sans étudier (x=0). Cette valeur doit être interprétée avec prudence car elle peut sortir du domaine de validité du modèle.

Prévisions et limites ⚠️

Utilisation pour les prévisions

La droite de régression permet de faire des prévisions. Par exemple, pour 7 heures d’étude :

$y = 1,6 \times 7 + 4 = 15,2$

On peut prévoir une note d’environ 15,2/20.

Limites de la régression linéaire

Elle suppose une relation linéaire entre les variables
Les prévisions en dehors de l’intervalle observé sont risquées
Elle ne prouve pas une relation de cause à effet
Elle est sensible aux valeurs aberrantes

Applications pratiques 🏫

La régression linéaire est utilisée dans de nombreux domaines :

Économétrie : relation entre prix et demande
Médecine : relation entre dose de médicament et effet
Psychologie : relation entre temps de pratique et performance
Marketing : relation entre budget publicitaire et ventes

Cas d’étude économique 💰

Une entreprise étudie la relation entre ses dépenses publicitaires (en milliers d’euros) et son chiffre d’affaires (en millions d’euros) :

Droite de régression obtenue : CA = 0,8 × Pub + 2,5

Cela signifie que chaque 1000€ dépensés en publicité génère en moyenne 800€ de chiffre d’affaires supplémentaire.

Récapitulatif mnémotechnique 🧠

Regression = Relier deux variables

a = pente = variation de y quand x augmente de 1

b = valeur de y quand x=0

Pensez à a comme augmentation et b comme base !