Proportions et taux d'évolution | Kilasy

Accueil » Leçons » Proportions et taux d’évolution

Statistiques descriptives

Les proportions sont des outils fondamentaux en statistiques qui permettent de mesurer la part d’un sous-ensemble dans un ensemble plus large. Elles sont particulièrement utiles pour comparer des groupes de tailles différentes.

Définition et calcul d’une proportion

Une proportion représente la part d’une catégorie spécifique dans l’ensemble de la population. Elle se calcule avec la formule suivante :

$p = \frac{n}{N}$

Où :

p est la proportion
n est l’effectif de la catégorie étudiée
N est l’effectif total de la population

Exemple concret 🎯

Imaginons une classe de 30 élèves dont 18 filles. La proportion de filles dans cette classe est :

$p = \frac{18}{30} = 0,6$

Cela signifie que 60% des élèves sont des filles. On peut aussi exprimer cette proportion sous forme de pourcentage en multipliant par 100.

Taux d’évolution 📈

Le taux d’évolution mesure la variation relative d’une grandeur entre deux dates. C’est un indicateur essentiel pour analyser des évolutions dans le temps.

Formule du taux d’évolution

Le taux d’évolution se calcule avec la formule :

$t = \frac{V_{\text{finale}} - V_{\text{initiale}}}{V_{\text{initiale}}} \times 100$

Où :

t est le taux d’évolution en pourcentage
V_initiale est la valeur de départ
V_finale est la valeur d’arrivée

Exemple d’application 💡

Supposons qu’une entreprise ait réalisé un chiffre d’affaires de 50 000€ l’année dernière et de 65 000€ cette année. Le taux d’évolution est :

$t = \frac{65000 - 50000}{50000} \times 100 = 30\%$

L’entreprise a donc connu une augmentation de 30% de son chiffre d’affaires.

Taux d’évolution réciproque 🔄

Lorsqu’on connaît le taux d’évolution, on peut calculer le taux réciproque pour retrouver la valeur initiale :

$t_{\text{reciproque}} = \frac{100}{100 + t} \times 100 - 100$

Reprenons notre exemple avec une augmentation de 30% :

$t_{\text{reciproque}} = \frac{100}{100 + 30} \times 100 - 100 = -23,08\%$

Pour revenir de 65 000€ à 50 000€, il faudrait une baisse de 23,08%.

Représentation graphique 📉

Voici une représentation de l’évolution du chiffre d’affaires sur 5 ans :

Rendered by QuickLaTeX.com

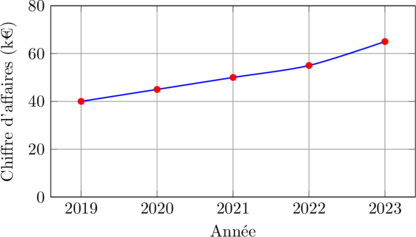
Applications pratiques 🏢

Les proportions et taux d’évolution sont utilisés dans de nombreux domaines :

Économie : analyse de l’inflation, croissance du PIB
Marketing : part de marché, taux de conversion
Démographie : taux de natalité, proportion de population active
Éducation : taux de réussite, proportion de filles/garçons

Cas d’étude complet 📋

Une ville compte 25 000 habitants. En 2020, 15 000 personnes étaient actives. En 2023, ce nombre est passé à 16 500.

Proportion d’actifs en 2020 :

$p_{2020} = \frac{15000}{25000} = 0,6$

(60%)

Proportion d’actifs en 2023 :

$p_{2023} = \frac{16500}{25000} = 0,66$

(66%)

Taux d’évolution de la proportion :

$t = \frac{0,66 - 0,60}{0,60} \times 100 = 10\%$

La proportion d’actifs a donc augmenté de 10% sur cette période.

Récapitulatif mnémotechnique 🧠

PROPORTION = Part / Total

TAUX = (Nouveau – Ancien) / Ancien × 100

Pensez à Pour Tous pour la proportion, et Toujours Analyser les Variations pour le taux !