Une suite numérique est une liste ordonnée de nombres qui suivent une certaine règle de formation. La monotonie d’une suite décrit son comportement : est-ce qu’elle augmente, diminue, ou reste constante ?

Une suite (uₙ) est dite :

• Croissante si pour tout n, uₙ₊₁ ≥ uₙ
• Décroissante si pour tout n, uₙ₊₁ ≤ uₙ
• Strictement croissante si uₙ₊₁ > uₙ
• Strictement décroissante si uₙ₊₁ < uₙ
• Constante si uₙ₊₁ = uₙ pour tout n

📈 Méthodes pour étudier la monotonie

Pour déterminer si une suite est croissante ou décroissante, on peut utiliser plusieurs méthodes :

Méthode 1 : Calcul de la différence

On calcule uₙ₊₁ – uₙ :

• Si uₙ₊₁ – uₙ > 0 → suite croissante
• Si uₙ₊₁ – uₙ < 0 → suite décroissante
• Si uₙ₊₁ – uₙ = 0 → suite constante

Exemple : Soit la suite uₙ = 2n + 1

uₙ₊₁ – uₙ = [2(n+1) + 1] – [2n + 1] = 2n + 2 + 1 – 2n – 1 = 2 > 0

Donc la suite est strictement croissante.

Méthode 2 : Rapport pour les suites à termes positifs

Pour uₙ > 0, on calcule uₙ₊₁/uₙ :

• Si uₙ₊₁/uₙ > 1 → suite croissante
• Si uₙ₊₁/uₙ < 1 → suite décroissante

📊 Représentation graphique de la monotonie

Voici une représentation visuelle des différents types de monotonie :

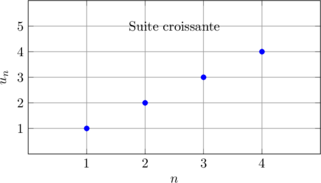
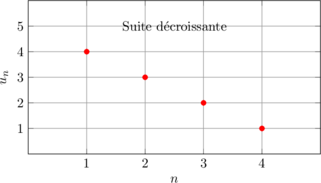
🎯 Notion de bornes d’une suite

Une suite peut être bornée ou non bornée :

Suite majorée : Il existe un nombre M tel que uₙ ≤ M pour tout n

Suite minorée : Il existe un nombre m tel que uₙ ≥ m pour tout n

Suite bornée : Elle est à la fois majorée et minorée

Exemple : La suite uₙ = (-1)ⁿ/n

Cette suite est bornée car pour tout n ≥ 1 :

-1 ≤ uₙ ≤ 1

Elle est majorée par 1 et minorée par -1.

🔍 Méthode pour trouver les bornes

Pour déterminer si une suite est bornée :

1. Étudier les variations de la suite
2. Chercher un majorant/mineurant évident
3. Utiliser des inégalités pour encadrer la suite

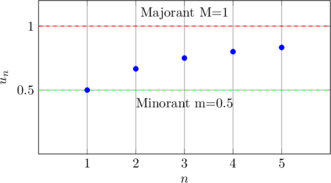
Exemple : uₙ = n/(n+1)

On peut écrire : uₙ = 1 – 1/(n+1)

Comme 1/(n+1) > 0, on a uₙ < 1

Et comme uₙ ≥ 1/2 pour n ≥ 1, la suite est bornée.

💡 Astuce mnémotechnique

Pour retenir les différents types de monotonie :

« Croissant comme le soleil qui monte, décroissant comme le soleil qui descend »

Et pour les bornes : « Majoré = Maximum possible, Minoré = Minimum possible »