Une primitive d’une fonction f est une fonction F dont la dérivée est égale à f. Autrement dit, si F'(x) = f(x) pour tout x dans un intervalle, alors F est une primitive de f.

Exemple simple : Si f(x) = 2x, alors F(x) = x² est une primitive de f car la dérivée de x² est bien 2x.

📚 Primitives des fonctions usuelles

Voici les primitives des fonctions de base que tu dois absolument connaître :

• Fonction constante : f(x) = k → F(x) = kx + C
• Fonction puissance : f(x) = xⁿ → F(x) = xⁿ⁺¹/(n+1) + C (pour n ≠ -1)
• Fonction inverse : f(x) = 1/x → F(x) = ln|x| + C
• Fonction exponentielle : f(x) = eˣ → F(x) = eˣ + C
• Fonctions trigonométriques : f(x) = cos(x) → F(x) = sin(x) + C

La constante C est très importante ! Elle représente l’infinité de primitives possibles.

🧮 Calcul pratique de primitives

Exemple 1 : Trouver une primitive de f(x) = 3x² + 2x – 5

On applique les règles de base :

Exemple 2 : Primitive de f(x) = 4eˣ + 1/x

🔍 Vérification d’une primitive

Pour vérifier qu’une fonction F est bien une primitive de f, il suffit de dériver F et de vérifier qu’on obtient f.

Exemple : Vérifier que F(x) = sin(x) + x² est une primitive de f(x) = cos(x) + 2x

Dérivons F : F'(x) = cos(x) + 2x qui est bien égal à f(x) ✅

📈 Représentation graphique

Les différentes primitives d’une fonction correspondent à des courbes décalées verticalement. Voici une illustration :

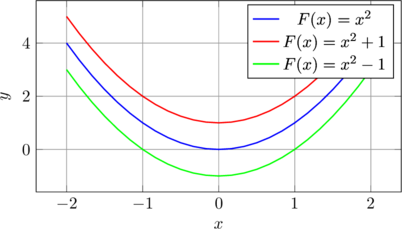
💡 Astuce mnémotechnique

Pour retenir les primitives usuelles, pensez à la dérivation inverse : « La primitive, c’est la dérivée à l’envers ! » 🔄

Récapitulatif : Une primitive est une fonction dont la dérivée donne la fonction de départ. N’oubliez jamais la constante d’intégration C !