Asymptotes et positions relatives | Kilasy

Accueil » Leçons » Asymptotes et positions relatives

Étude globale des fonctions

🎯 Introduction aux asymptotes

Les asymptotes sont des droites vers lesquelles une fonction se rapproche sans jamais les toucher (ou très rarement). Elles nous aident à comprendre le comportement d’une fonction aux limites de son domaine de définition. 📈

🔍 Les différents types d’asymptotes

Il existe trois types principaux d’asymptotes :

Asymptote verticale : lorsque x tend vers une valeur finie
Asymptote horizontale : lorsque x tend vers l’infini
Asymptote oblique : lorsque la fonction se comporte comme une droite non horizontale

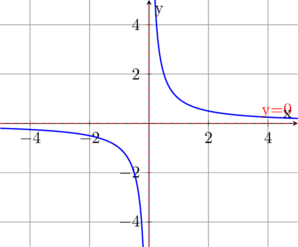
📐 Asymptote verticale

Une droite d’équation x = a est asymptote verticale à la courbe si :

$\lim_{x \to a^-} f(x) = \pm \infty$

ou

$\lim_{x \to a^+} f(x) = \pm \infty$

Exemple : Soit la fonction f(x) = 1/(x-2)

Quand x → 2⁺, f(x) → +∞

Quand x → 2⁻, f(x) → -∞

Donc x = 2 est asymptote verticale.

➖ Asymptote horizontale

Une droite d’équation y = b est asymptote horizontale si :

$\lim_{x \to +\infty} f(x) = b$

ou

$\lim_{x \to -\infty} f(x) = b$

Exemple : f(x) = (2x+1)/(x+3)

$\lim_{x \to \infty} \frac{2x+1}{x+3} = 2$

Donc y = 2 est asymptote horizontale.

↗️ Asymptote oblique

Une droite d’équation y = ax + b est asymptote oblique si :

$\lim_{x \to \infty} [f(x) - (ax + b)] = 0$

Pour trouver a et b :

$a = \lim_{x \to \infty} \frac{f(x)}{x}$

$b = \lim_{x \to \infty} [f(x) - ax]$

Exemple : f(x) = (x²+1)/x

$a = \lim_{x \to \infty} \frac{x^2+1}{x^2} = 1$

$b = \lim_{x \to \infty} [\frac{x^2+1}{x} - x] = \lim_{x \to \infty} \frac{1}{x} = 0$

Donc y = x est asymptote oblique.

📊 Positions relatives

Pour étudier la position relative entre la courbe et son asymptote, on étudie le signe de f(x) – (ax + b).

Astuce mnémotechnique : Pensez aux asymptotes comme des « guides » qui orientent le tracé de la courbe. 🧭

Rendered by QuickLaTeX.com