🎯 Introduction aux théorèmes des accroissements finis
Les théorèmes des accroissements finis sont des résultats fondamentaux qui établissent des liens entre la variation d’une fonction et sa dérivée. Ils sont essentiels pour l’analyse fonctionnelle et l’optimisation. 🔗
📏 Théorème des accroissements finis (TAF)
Si une fonction f est :
- Continue sur [a, b]
- Dérivable sur ]a, b[
Alors il existe au moins un réel c dans ]a, b[ tel que :
![]()
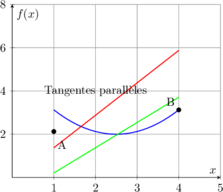
🔍 Interprétation géométrique
Le TAF assure qu’il existe au moins un point où la tangente est parallèle à la corde joignant les points (a, f(a)) et (b, f(b)).
✅ Exemple d’application
Soit f(x) = x³ sur [1, 3]. Vérifions le TAF :
f(1) = 1, f(3) = 27, f'(x) = 3x²
Pente de la corde : (27 – 1)/(3 – 1) = 13
On cherche c tel que 3c² = 13 ⇒ c² = 13/3 ⇒ c = √(13/3) ≈ 2.08
Ce point appartient bien à ]1, 3[.
📐 Théorème de Rolle (cas particulier du TAF)
Si une fonction f est :
- Continue sur [a, b]
- Dérivable sur ]a, b[
- f(a) = f(b)
Alors il existe au moins un réel c dans ]a, b[ tel que f'(c) = 0.
![]()
🔍 Application concrète
Un projectile lancé verticalement atteint sa hauteur maximale lorsque sa vitesse verticale s’annule. C’est une illustration du théorème de Rolle ! 🚀
🧮 Inégalité des accroissements finis
Si f est dérivable sur [a, b] et si sa dérivée est bornée : |f'(x)| ≤ M pour tout x dans [a, b]
Alors :
![]()
💡 Utilisation pratique
Cette inégalité permet de contrôler la variation d’une fonction connaissant une borne sur sa dérivée.
🔢 Applications numériques
Problème 1 : Encadrement d’une valeur
Soit f(x) = √x. Donner un encadrement de √101.
Sur [100, 101], f'(x) = 1/(2√x) donc |f'(x)| ≤ 1/20 = 0.05
Ainsi : |√101 – 10| ≤ 0.05 × 1 = 0.05
Donc : 9.95 ≤ √101 ≤ 10.05
Problème 2 : Unicité de solution
Montrer que l’équation x³ + x – 1 = 0 admet une unique solution dans [0, 1].
Soit f(x) = x³ + x – 1. On a f(0) = -1 et f(1) = 1.
Par le théorème des valeurs intermédiaires, il existe au moins une solution.
De plus, f'(x) = 3x² + 1 > 0 sur [0, 1], donc f est strictement croissante, d’où l’unicité. ✅
📊 Étude de variations
Le TAF permet d’étudier les variations d’une fonction :
- Si f'(x) > 0 sur un intervalle, alors f est strictement croissante
- Si f'(x) < 0 sur un intervalle, alors f est strictement décroissante
- Si f'(x) = 0 sur un intervalle, alors f est constante
🎨 Représentation graphique complète
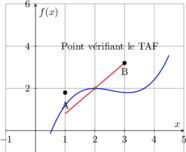
💡 Récapitulatif et astuces
Astuce mnémotechnique : « Le TAF, c’est comme une moyenne de vitesse instantanée égale à la vitesse moyenne » ! 🚗💨
Les théorèmes des accroissements finis sont des outils puissants pour :
- Démontrer des inégalités
- Étudier les variations de fonctions
- Résoudre des équations différentielles
- Faire des approximations numériques
Leur compréhension est essentielle pour la suite des études en mathématiques et en sciences.

