🎯 Qu’est-ce que la dérivée ?
La dérivée d’une fonction en un point mesure le taux de variation instantané de cette fonction. Géométriquement, elle représente la pente de la tangente à la courbe représentative de la fonction en ce point. 📐
La dérivée de f en a est définie par :
![]()
🔍 Exemple de calcul
Calculons la dérivée de f(x) = x² en x = 3 :
![]()
📚 Règles fondamentales de dérivation
1. Dérivée d’une constante
Si f(x) = k (constante), alors f'(x) = 0
![]()
2. Dérivée de xⁿ (puissance)
Si f(x) = xⁿ, alors f'(x) = nxⁿ⁻¹
![]()
Exemple : f(x) = x⁵ ⇒ f'(x) = 5x⁴
3. Dérivée d’une somme
![]()
4. Dérivée d’un produit
![]()
5. Dérivée d’un quotient
![]()
6. Dérivée d’une composée (règle de chaîne)
![]()
🔢 Tableau des dérivées usuelles
Voici les dérivées des fonctions les plus courantes :
| Fonction | Dérivée |
|---|---|
| f(x) = k (constante) | f'(x) = 0 |
| f(x) = xⁿ | f'(x) = nxⁿ⁻¹ |
| f(x) = √x | f'(x) = 1/(2√x) |
| f(x) = eˣ | f'(x) = eˣ |
| f(x) = ln(x) | f'(x) = 1/x |
| f(x) = sin(x) | f'(x) = cos(x) |
| f(x) = cos(x) | f'(x) = -sin(x) |
🧮 Exemples détaillés de dérivation
Exemple 1 : Fonction polynomiale
Soit f(x) = 3x⁴ – 2x³ + 5x – 7
Dérivée terme à terme :
![]()
Exemple 2 : Fonction rationnelle
Soit f(x) = (2x + 1)/(x – 3)
Appliquons la formule du quotient :
![]()
Exemple 3 : Fonction composée
Soit f(x) = (3x² + 1)⁴
On pose u(x) = 3x² + 1 donc f(x) = [u(x)]⁴
![]()
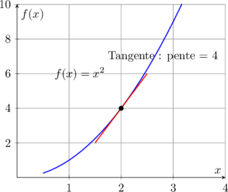
📈 Interprétation géométrique
Voici une illustration de la dérivée comme pente de la tangente :
💡 Récapitulatif
Astuce mnémotechnique : Pour la règle du produit, souvenez-vous de « dérivée première × deuxième + première × dérivée deuxième » ! 🧠
La maîtrise des règles de dérivation est essentielle pour étudier les variations des fonctions et résoudre de nombreux problèmes d’optimisation.

