Notion de limite et continuité

Accueil » Leçons » Notion de limite et continuité

Limites, continuité et dérivation

🎯 Introduction aux limites

La limite d’une fonction est un concept fondamental en analyse mathématique qui décrit le comportement d’une fonction lorsque sa variable s’approche d’une certaine valeur. 📈

Formellement, on dit que la limite de f(x) lorsque x tend vers a est L si on peut rendre f(x) aussi proche que l’on veut de L en prenant x suffisamment proche de a.

$\lim_{x \to a} f(x) = L$

🔍 Exemple concret

Soit la fonction f(x) = x². Que se passe-t-il lorsque x s’approche de 2 ?

Calculons quelques valeurs :

f(1.9) = 3.61
f(1.99) = 3.9601
f(2.01) = 4.0401
f(2.1) = 4.41

On observe que plus x se rapproche de 2, plus f(x) se rapproche de 4. Ainsi :

$\lim_{x \to 2} x^2 = 4$

📊 Limites à gauche et à droite

Il est important de distinguer la limite à gauche (lorsque x approche a par valeurs inférieures) et la limite à droite (lorsque x approche a par valeurs supérieures).

$\lim_{x \to a^-} f(x) = L_1$

$\lim_{x \to a^+} f(x) = L_2$

La limite existe si et seulement si L₁ = L₂.

⚠️ Exemple de discontinuité

Considérons la fonction définie par morceaux :

$f(x) = \begin{cases} x + 1 & \text{si } x < 0 \\ x - 1 & \text{si } x \geq 0 \end{cases}$

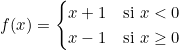
Limite à gauche en 0 :

$\lim_{x \to 0^-} f(x) = \lim_{x \to 0^-} (x + 1) = 1$

Limite à droite en 0 :

$\lim_{x \to 0^+} f(x) = \lim_{x \to 0^+} (x - 1) = -1$

Les limites sont différentes, donc la limite en 0 n’existe pas. ❌

🔗 La continuité

Une fonction f est continue en un point a si trois conditions sont satisfaites :

f(a) est définie
La limite de f(x) lorsque x tend vers a existe
La limite est égale à f(a)

$\lim_{x \to a} f(x) = f(a)$

✅ Exemple de fonction continue

La fonction f(x) = x³ est continue en tout point de ℝ car pour tout a réel :

$\lim_{x \to a} x^3 = a^3 = f(a)$

📈 Représentation graphique

Voici une illustration graphique des concepts de limite et continuité :

Rendered by QuickLaTeX.com

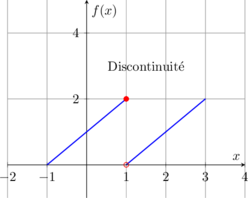
💡 Récapitulatif

Astuce mnémotechnique : Pour vérifier la continuité en un point, pensez au « test du crayon » : si vous pouvez tracer la fonction sans lever le crayon, elle est continue ! ✏️

Les limites nous permettent d’étudier le comportement des fonctions même aux points où elles ne sont pas définies, ce qui est essentiel pour l’analyse mathématique.