Toggle Side Panel
Contenu du cours
Leçons
0/3
Introduction aux systèmes linéaires
Résolution algébrique
Applications concrètes
Systèmes d’équations linéaires dans ℝ³

🌍 Applications réelles des systèmes linéaires

Les systèmes d’équations linéaires à trois inconnues trouvent des applications dans de nombreux domaines : physique, économie, ingénierie, informatique, et même dans la vie quotidienne ! Voyons quelques exemples concrets. 🚀

📈 Économie et gestion

Problème d’optimisation de production : Une entreprise produit trois articles A, B et C. Les contraintes sont :

  • La production totale ne doit pas dépasser 1000 unités
  • Le produit A nécessite 2h de main d’œuvre, B nécessite 3h, C nécessite 1h (total disponible : 2000h)
  • Le bénéfice unitaire est de 10€ pour A, 15€ pour B, et 8€ pour C

On veut maximiser le bénéfice total sous contraintes. Ce problème se modélise par un système d’inéquations qui peut être résolu par la méthode du simplexe, extension des systèmes linéaires.

⚖️ Équilibre de marché

En microéconomie, l’équilibre entre l’offre et la demande pour trois biens interconnectés peut être modélisé par un système. Par exemple :

\begin{cases} Q_{d1} = 100 - 2P_1 + P_2 - P_3 \\ Q_{d2} = 80 + P_1 - 3P_2 + 2P_3 \\ Q_{d3} = 120 - P_1 + P_2 - 2P_3 \end{cases}

\begin{cases} Q_{s1} = 20 + 3P_1 \\ Q_{s2} = 40 + 2P_2 \\ Q_{s3} = 30 + P_3 \end{cases}

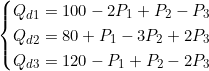
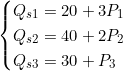
À l’équilibre, Q_d = Q_s pour chaque bien, ce qui donne un système de trois équations à trois inconnues (P₁, P₂, P₃).

🔬 Physique et ingénierie

Résistance des matériaux : Dans une structure triangulaire, les forces aux nœuds obéissent à l’équilibre statique :

\begin{cases} F_1\cos\theta_1 + F_2\cos\theta_2 + F_3\cos\theta_3 = 0 \\ F_1\sin\theta_1 + F_2\sin\theta_2 + F_3\sin\theta_3 = 0 \\ F_1d_1 + F_2d_2 + F_3d_3 = M \end{cases}

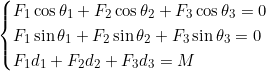
Ce système permet de calculer les forces F₁, F₂, F₃ dans les membrures.

Circuit électrique : Dans un circuit avec trois mailles, les lois de Kirchhoff donnent :

\begin{cases} I_1 - I_2 - I_3 = 0 \\ R_1I_1 + R_2I_2 = V_1 \\ R_2I_2 - R_3I_3 = V_2 \end{cases}

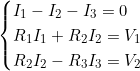
Un exemple numérique avec R₁=2Ω, R₂=3Ω, R₃=1Ω, V₁=12V, V₂=6V :

\begin{cases} I_1 - I_2 - I_3 = 0 \\ 2I_1 + 3I_2 = 12 \\ 3I_2 - I_3 = 6 \end{cases}

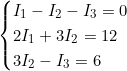
La solution est I₁ = 3A, I₂ = 2A, I₃ = 1A.

🖥️ Graphisme 3D et vision par ordinateur

Les systèmes linéaires sont fondamentaux en infographie pour :

  • La transformation et rotation des objets 3D
  • Le calcul des intersections rayons-surfaces
  • L’interpolation des couleurs et textures
  • La résolution de systèmes pour l’éclairage et l’ombrage

Chaque transformation 3D peut être représentée par une matrice 3×3 appliquée aux coordonnées (x, y, z).

🧪 Chimie : équilibrage d’équations

Pour équilibrer une réaction chimique comme : aCH₄ + bO₂ → cCO₂ + dH₂O

On écrit les équations d’équilibre atomique :

\begin{cases} \text{Carbone : } a = c \\ \text{Hydrogène : } 4a = 2d \\ \text{Oxygène : } 2b = 2c + d \end{cases}

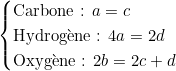
Ce qui donne le système :

\begin{cases} a - c = 0 \\ 4a - 2d = 0 \\ 2b - 2c - d = 0 \end{cases}

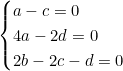
Une solution est a=1, b=2, c=1, d=2, donc CH₄ + 2O₂ → CO₂ + 2H₂O

📊 Visualisation des applications

Voici comment un système peut modéliser l’intersection de trois plans représentant différentes contraintes :

Rendered by QuickLaTeX.com

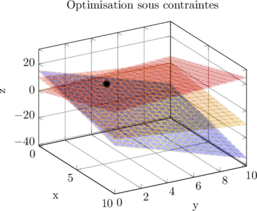
💡 Astuce mnémotechnique

Pour retenir les domaines d’application, pensez à « CEPHIR » :

  • Chimie
  • Économie
  • Physique
  • Ingénierie
  • Informatique
  • Recherche opérationnelle

🔮 Conclusion et perspectives

Les systèmes linéaires 3×3 sont la porte d’entrée vers des concepts plus avancés : espaces vectoriels, algèbre linéaire, optimisation, et même l’apprentissage automatique où les réseaux de neurones peuvent être vus comme des systèmes linéaires gigantesques !

La maîtrise de ces fondamentaux ouvre des horizons dans de nombreuses disciplines scientifiques et techniques. 🌟

Précédent
Suivant