Calculs de probabilités

Accueil » Leçons » Calculs de probabilités

Probabilités

Maîtriser les calculs probabilistes 📊

Maintenant que nous connaissons le vocabulaire de base, voyons comment calculer concrètement des probabilités dans diverses situations.

Probabilités conditionnelles

La probabilité conditionnelle mesure la probabilité qu’un événement A se réalise sachant qu’un événement B est déjà réalisé. Elle se note P(A|B) et se calcule ainsi : $P(A|B) = \frac{P(A \cap B)}{P(B)} \quad \text{avec} \quad P(B) \neq 0$ Exemple : Dans une classe de 30 élèves, 18 filles et 12 garçons. 10 filles et 4 garçons pratquent le tennis. Quelle est la probabilité qu’un élève pratiquant le tennis soit une fille ? • A = « être une fille » • B = « pratiquer le tennis » $P(A|B) = \frac{P(A \cap B)}{P(B)} = \frac{10/30}{14/30} = \frac{10}{14} = \frac{5}{7}$

Formule des probabilités totales

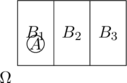
Si les événements B₁, B₂, …, Bₙ forment une partition de Ω (ils sont incompatibles deux à deux et leur réunion donne Ω), alors pour tout événement A : $P(A) = P(A \cap B_1) + P(A \cap B_2) + ... + P(A \cap B_n)$ Ou encore : $P(A) = P(A|B_1)P(B_1) + P(A|B_2)P(B_2) + ... + P(A|B_n)P(B_n)$

Représentation visuelle :

Rendered by QuickLaTeX.com

Exemple d’application

Une usine possède trois machines produisant le même objet : M₁ (50% de production), M₂ (30%), M₃ (20%). Les taux de défauts sont : 2% pour M₁, 3% pour M₂, 5% pour M₃. Quelle est la probabilité qu’un objet pris au hasard soit défectueux ?

Soit D = « l’objet est défectueux » $P(D) = P(D|M_1)P(M_1) + P(D|M_2)P(M_2) + P(D|M_3)P(M_3)$ $P(D) = (0.02 \times 0.5) + (0.03 \times 0.3) + (0.05 \times 0.2) = 0.01 + 0.009 + 0.01 = 0.029$

Arbre de probabilités

Les arbres pondérés sont très utiles pour visualiser et calculer des probabilités, surtout quand plusieurs événements se succèdent :

Rendered by QuickLaTeX.com

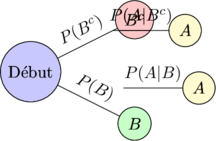
Sur les branches, on inscrit les probabilités conditionnelles. La probabilité d’un chemin est le produit des probabilités le long des branches.

Formule de Bayes

Cette formule permet de « inverser » les conditionnements : $P(B|A) = \frac{P(A|B) \times P(B)}{P(A)}$ Reprenons l’exemple de l’usine : Sachant qu’un objet est défectueux, quelle est la probabilité qu’il provienne de la machine M₁ ? $P(M_1|D) = \frac{P(D|M_1) \times P(M_1)}{P(D)} = \frac{0.02 \times 0.5}{0.029} \approx 0.3448$

Récapitulatif méthodologique

Pour résoudre un problème de probabilités :

Bien définir l’univers Ω et les événements
Représenter la situation (diagramme, arbre)
Identifier si les événements sont incompatibles/indépendants
Choisir la formule adaptée
Calculer méthodiquement
Vérifier que le résultat est cohérent (entre 0 et 1)

Avec de la pratique, ces calculs deviendront naturels ! 💪