Les différentes équations d’un plan 📏
Un plan dans l’espace peut être défini de plusieurs manières.
La plus courante est l’équation cartésienne : ![]() où a, b, c sont les coordonnées d’un vecteur normal
où a, b, c sont les coordonnées d’un vecteur normal ![]() au plan.
au plan.
Un plan peut aussi être défini par un point A(x₀, y₀, z₀) et deux vecteurs directeurs ![]() et
et ![]() non colinéaires.
non colinéaires.
Son équation paramétrique est alors : 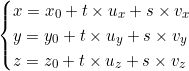 avec t et s paramètres réels.
avec t et s paramètres réels.
Exemple de détermination d’équation de plan 🎯
Soit un plan P passant par les points A(1, 0, 2), B(2, 1, 1) et C(0, 1, 3). Pour trouver son équation cartésienne :
- Calculer deux vecteurs directeurs :
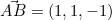 et
et 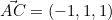
- Calculer leur produit vectoriel pour obtenir un vecteur normal :
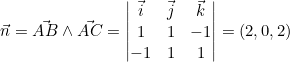
3. L’équation du plan est donc : 2(x – 1) + 0(y – 0) + 2(z – 2) = 0, soit 2x + 2z – 6 = 0 ou x + z – 3 = 0.
Positions relatives de deux plans 🔀
Deux plans peuvent être :
- Parallèles strictement : aucun point commun, vecteurs normaux colinéaires
- Confondus : tous points communs, mêmes équations
- Sécants : intersection selon une droite
Soient deux plans d’équations : P₁: a₁x + b₁y + c₁z + d₁ = 0 et P₂: a₂x + b₂y + c₂z + d₂ = 0. Ils sont parallèles si : ![]()
Ils sont sécants si leurs vecteurs normaux ne sont pas colinéaires.
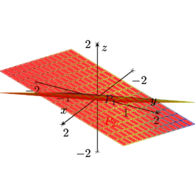
Représentation graphique de plans 📊
Voici une représentation de deux plans sécants :
Distance d’un point à un plan 📐
La distance d’un point M(x₀, y₀, z₀) à un plan P: ax + by + cz + d = 0 est donnée par : ![]()
Exemple : Distance du point M(1, 2, 3) au plan P: 2x – y + 2z – 4 = 0 : ![]()
Astuce mnémotechnique 🧠
Pour retenir la formule de distance point-plan : « Valeur absolue sur racine carrée, la distance est toujours bien calculée! ».

