Forme trigonométrique d’un nombre complexe 🔄
Tout nombre complexe non nul z peut s’écrire sous forme trigonométrique :
![]()
où |z| est le module et θ = arg(z) est l’argument de z.
Exemple :
Pour z = 1 + i√3, on a |z| = 2 et arg(z) = π/3, donc :
![]()
Forme exponentielle d’un nombre complexe 🚀
La forme exponentielle utilise la formule d’Euler :
![]()
Ainsi, tout nombre complexe non nul z peut s’écrire :
![]()
où θ = arg(z).
Exemple :
Pour z = 1 + i, on a |z| = √2 et arg(z) = π/4, donc :
![]()
Conversion entre les différentes formes 🔁
Pour passer de la forme algébrique z = a + ib à la forme exponentielle :
- Calculer le module :
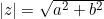
- Déterminer l’argument θ tel que :
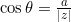 et
et 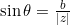
- Écrire :
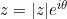
Exemple complet :
Convertir z = -√3 + i en forme exponentielle :
Module : ![]()
Argument : ![]() et
et ![]()
Donc θ = 5π/6 (2ème quadrant)
Forme exponentielle : ![]()
Avantages de la forme exponentielle ⚡
La forme exponentielle simplifie considérablement les calculs :
Multiplication : ![]()
Division : ![]()
Puissance n-ième (Formule de Moivre) : ![]()
Racine n-ième : ![]() pour k = 0, 1, …, n-1
pour k = 0, 1, …, n-1
Application : calcul de puissances 🎯
Calculons (1 + i)¹⁰ en utilisant la forme exponentielle :
D’abord, convertissons 1 + i en forme exponentielle :
![]()
![]()
Donc : ![]()
Maintenant : ![]()
Car ![]() (période 2π)
(période 2π)
Finalement : ![]()
Représentation graphique des formes 📈
Les différentes formes d’un nombre complexe correspondent à différentes manières de repérer un point dans le plan :
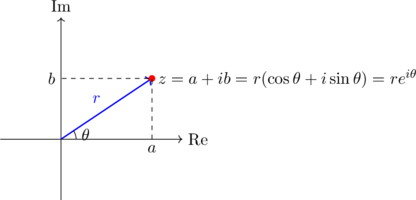
Astuce mnémotechnique 💡
Pour retenir la formule d’Euler : « Euler unit cosinus et sinus dans l’exponentielle imaginaire ». Pour les conversions : « Module = distance, Argument = angle ».

