Opérations de base, modules et arguments

Accueil » Leçons » Opérations de base, modules et arguments

Nombres complexes

Introduction aux nombres complexes 🧮

Un nombre complexe est un nombre qui s’écrit sous la forme z = a + ib, où :

a est la partie réelle (notée Re(z))
b est la partie imaginaire (notée Im(z))
i est le nombre imaginaire tel que i² = -1

L’ensemble des nombres complexes est noté ℂ.

Opérations fondamentales ➕➖✖️➗

Soient deux nombres complexes z = a + ib et z’ = a’ + ib’ :

Addition : z + z’ = (a + a’) + i(b + b’)

Soustraction : z – z’ = (a – a’) + i(b – b’)

Multiplication : z × z’ = (aa’ – bb’) + i(ab’ + a’b)

Division : z/z’ = [(aa’ + bb’)/(a’² + b’²)] + i[(a’b – ab’)/(a’² + b’²)]

Exemple concret :

Soit z = 3 + 2i et z’ = 1 – i

z + z’ = (3 + 1) + i(2 – 1) = 4 + i

z × z’ = (3×1 – 2×(-1)) + i(3×(-1) + 2×1) = (3 + 2) + i(-3 + 2) = 5 – i

Module d’un nombre complexe 📏

Le module d’un nombre complexe z = a + ib est noté |z| et vaut :

$\lvert z \rvert = \sqrt{a^2 + b^2}$

Le module représente la distance entre l’origine du plan complexe et le point d’affixe z.

Exemple :

Pour z = 3 + 4i, le module est :

$\lvert z \rvert = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5$

Argument d’un nombre complexe 🧭

L’argument d’un nombre complexe non nul z = a + ib est l’angle θ tel que :

$\cos\theta = \frac{a}{\lvert z \rvert} \quad \text{et} \quad \sin\theta = \frac{b}{\lvert z \rvert}$

On note arg(z) = θ modulo 2π.

Exemple :

Pour z = 1 + i, le module est √2 et l’argument est π/4 car :

$\cos(\pi/4) = \frac{1}{\sqrt{2}} \quad \text{et} \quad \sin(\pi/4) = \frac{1}{\sqrt{2}}$

Représentation géométrique 📊

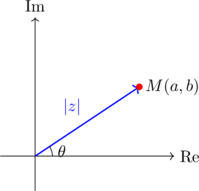
Chaque nombre complexe z = a + ib peut être représenté par un point M de coordonnées (a, b) dans le plan. Le module |z| correspond à la distance OM et l’argument arg(z) à l’angle entre l’axe des réels et le vecteur OM.

Rendered by QuickLaTeX.com

Propriétés importantes 🔑

Pour tous nombres complexes z et z’ :

|z × z’| = |z| × |z’|
|z/z’| = |z|/|z’| (si z’ ≠ 0)
arg(z × z’) = arg(z) + arg(z’) modulo 2π
arg(z/z’) = arg(z) – arg(z’) modulo 2π

Conjugué d’un nombre complexe 🔄

Le conjugué de z = a + ib est noté ̅z et vaut ̅z = a – ib.

Propriétés :

z + ̅z = 2Re(z)
z – ̅z = 2iIm(z)
z × ̅z = |z|²
|̅z| = |z|
arg(̅z) = -arg(z) modulo 2π

Astuce mnémotechnique 💡

Pour retenir la multiplication : « Comme une double distributivité, mais i² = -1 ». Pour les arguments : « Multiplication = addition, Division = soustraction ».