Critères de convergence 🎯

Théorème des gendarmes (ou d’encadrement) 👮

Soient (aₙ), (bₙ) et (cₙ) trois suites telles que :

∃ N ∈ ℕ, ∀ n ≥ N, aₙ ≤ bₙ ≤ cₙ

Si (aₙ) et (cₙ) convergent vers la même limite L, alors (bₙ) converge aussi vers L.

Exemple d’application 📝

Déterminons la limite de la suite uₙ = (sin n)/n

On sait que ∀ n ∈ ℕ, -1 ≤ sin n ≤ 1

Donc -1/n ≤ (sin n)/n ≤ 1/n

Comme lim(-1/n) = 0 et lim(1/n) = 0, par le théorème des gendarmes :

Suites divergentes 🚫

Une suite peut diverger de plusieurs manières :

• Divergence vers +∞ : ∀ M > 0, ∃ N ∈ ℕ tel que ∀ n ≥ N, uₙ > M
• Divergence vers -∞ : ∀ M < 0, ∃ N ∈ ℕ tel que ∀ n ≥ N, uₙ < M
• Divergence sans limite infinie : la suite n’a pas de limite (ex: uₙ = (-1)ⁿ)

Théorème de divergence 📚

Si une suite est croissante et non majorée, alors elle diverge vers +∞

Si une suite est décroissante et non minorée, alors elle diverge vers -∞

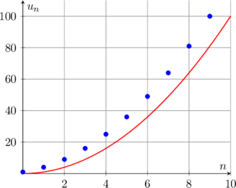
Suites adjacentes et convergence 🔗

Deux suites (aₙ) et (bₙ) sont dites adjacentes si :

1. (aₙ) est croissante
2. (bₙ) est décroissante
3. lim(bₙ – aₙ) = 0

Théorème : Si deux suites sont adjacentes, alors elles convergent vers la même limite.

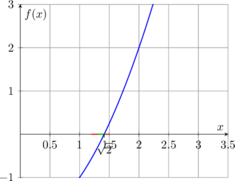
Application classique : méthode de dichotomie 🎯

Pour approcher la solution d’une équation f(x) = 0, on construit deux suites adjacentes qui encadrent la solution.

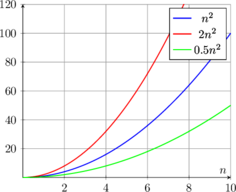
Comparaison des suites et limites infinies ⚖️

On peut comparer le comportement asymptotique des suites :

Relations de comparaison :

• uₙ ∼ vₙ si lim(uₙ/vₙ) = 1
• uₙ = o(vₙ) si lim(uₙ/vₙ) = 0
• uₙ = O(vₙ) si ∃ M > 0, |uₙ| ≤ M|vₙ| à partir d’un certain rang

Astuce mnémotechnique 🧠

Pour retenir le théorème des gendarmes, imaginez deux policiers (les suites qui encadrent) escortant un suspect (la suite du milieu). Si les deux policiers vont au même endroit (la même limite), le suspect n’a pas d’autre choix que de les suivre !