Introduction aux suites numériques 📈

Une suite numérique est une fonction définie sur l’ensemble des entiers naturels (ou une partie de celui-ci) à valeurs dans ℝ. On note généralement une suite (uₙ) où n ∈ ℕ.

Il existe deux principales façons de définir une suite :

• Suite définie explicitement : uₙ = f(n) où f est une fonction
• Suite définie par récurrence : uₙ₊₁ = f(uₙ) avec une valeur initiale u₀

Exemples de suites 🧮

Suite arithmétique : uₙ = u₀ + n × r

Suite géométrique : uₙ = u₀ × qⁿ

Le raisonnement par récurrence 🔁

Le raisonnement par récurrence est une méthode de démonstration essentielle pour les suites. Il comporte trois étapes :

1. Initialisation : Vérifier que la propriété est vraie au rang initial (généralement n = 0)
2. Hérédité : Démontrer que si la propriété est vraie à un rang n, alors elle est vraie au rang n+1
3. Conclusion : La propriété est vraie pour tout entier naturel n

Exemple d’application 💡

Montrons par récurrence que pour tout n ∈ ℕ, 1 + 2 + 3 + … + n = n(n+1)/2

Initialisation : Pour n = 0, 0 = 0(0+1)/2 = 0 ✓

Hérédité : Supposons que 1 + 2 + … + n = n(n+1)/2 (hypothèse de récurrence)

Alors 1 + 2 + … + n + (n+1) = n(n+1)/2 + (n+1) = (n+1)(n/2 + 1) = (n+1)(n+2)/2

La propriété est donc vraie au rang n+1

Conclusion : La formule est vraie pour tout n ∈ ℕ

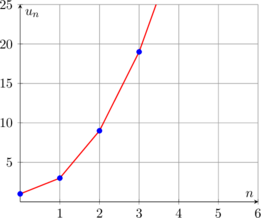
Représentation graphique d’une suite 📊

Une suite peut être représentée graphiquement de deux manières :

• Comme une fonction discrète : points de coordonnées (n, uₙ)
• Par un « escalier » pour les suites récurrentes

Astuce mnémotechnique 🧠

Pour retenir les trois étapes du raisonnement par récurrence, pensez à « I.H.C » : Initialisation, Hérédité, Conclusion. C’est comme conduire une voiture : on Initialise le moteur, on passe les vitesses (Hérédité), et on arrive à Conclusion !